Sur les valeurs propres d'une matrice aléatoire
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
oral HEC, BL - 2022 - Exercice sans préparation.
Soit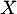 et
et 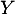 deux variables aléatoires indépendantes dfinies sur le même espace probabilisé
deux variables aléatoires indépendantes dfinies sur le même espace probabilisé 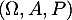 , suivant la même loi géométrique de paramètre
, suivant la même loi géométrique de paramètre ![$p\in]0, 1[$](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2/4.png) .
.
Pour tout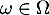 , on pose
, on pose
![\[A(\omega)=\lp\begin{array}{cc}X(\omega)&Y(\omega)\\Y(\omega)&X(\omega)\enar\rp\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2/6.png)
Soit
Pour tout
- Déterminer la probabilité que
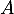 soit inversible.
soit inversible.
- Soit
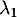 et
et 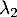 les variables aléatoires égales aux valeurs propres de
les variables aléatoires égales aux valeurs propres de 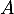 .
Calculer
.
Calculer 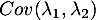 .
.
Correction
Correction
oral HEC, BL - 2022 - Exercice sans préparation.- La matrice est inversible si seulement si son déterminant est non nul, soit
![\[\det(A(\omega))=X^2(\omega)-Y^2(\omega)\not=0\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/1.png)
et donc, puisque ces variables aléatoires suivent des lois géométriques, donc en particulier sont à valeurs positives, on à donc que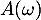 est inversible si et seulement si
est inversible si et seulement si
![\[X(\omega)\not=Y(\omega)\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/3.png)
La probabilité que cela arrive est
![\[P(X\not=Y) = 1 - P(X=Y)\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/4.png)
avec
![\[P(X=Y)=\sum_{k=1}^{+\infty}P((X=k)\cap(Y=k))\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/5.png)
soit, par indépendance des deux variables,
![\[\begin{array}{ll}
P(X=Y)&=\dsp\sum_{k=1}^{+\infty}P((X=k)\cap(Y=k))\\
&=\dsp\sum_{k=1}^{+\infty}\left( pq^{k-1}\rp^2\\
&=\dsp\sum_{k=1}^{+\infty}p^2(q^2)^{k-1}\\
&=\dfrac{p^2}{1-q^2}=\dfrac{p}{2-p}\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/6.png)
On obtient alors finalement la porbabilité
![\[\begin{array}{ll}P(X=Y)&=1-\dfrac{p}{2-p}\\&=\dfrac{2(1-p)}{2-p}\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/7.png)
- Les valeurs propres de
 sont les réels
sont les réels 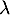 tels que
la matrice
tels que
la matrice
![\[A-\lambda I_2 =
\lp\begin{array}{cc}X(\omega)-\lambda&Y(\omega)\\Y(\omega)&X(\omega)-\lambda\enar\rp\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/10.png)
n'est pas inversible. On retrouve le raisonnement de la question précédente: le déterminant de cette matrice doit être nul, c'est-à-dire
![\[(X-\lambda)^2-Y^2=0\iff \lambda=X\pm Y\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/11.png)
On a donc nos deux valeurs propres
![\[\lambda_1=X(\omega)+Y(\omega)\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/12.png)
et
![\[\lambda_2=X(\omega)-Y(\omega)\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/13.png)
(ce qui montre au passage que cette matrice est toujours diagonalisable, car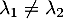 sauf si
sauf si 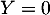 , dernier cas dans lequel la matrice est déjà diagonale)
, dernier cas dans lequel la matrice est déjà diagonale)
On calcule alors la covariance recherchée:
![\[Cov(\lambda_1,\lambda_2)=Cov(X+Y,X-Y)
=E\bigl((X+Y)(X-Y)\bigr)-E(X+Y)E(X-Y)\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/16.png)
soit, en développant avec la linéarité de l'espérance,
![\[Cov(\lambda_1,\lambda_2)=V(X)-V(Y)=0\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.2_c/17.png)
car ces deux variables aléatoires suivent la même loi.
Attention: on ne peut pas en déduire que les varaiables aléatoires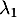 et
et 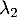 sont indépendantes.
sont indépendantes.
Au contraire même, vu leurs expressions, elles ne semblent pas indépendantes, à démontrer …
Tag:Variables aléatoires continues
Autres sujets au hasard:
