Racine carrée d'une loi exponentielle (bis)
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
HEC B/L - 2022 - Exercice sans préparation.
Soit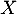 une variable aléatoire de densité
une variable aléatoire de densité 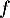 paire et continue sur
paire et continue sur 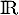 .
On suppose que
.
On suppose que  suit la loi exponentielle de paramètre
suit la loi exponentielle de paramètre 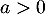 .
.
Soit
- On note
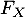 la fonction de répartition de
la fonction de répartition de 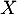 .
Montrer que pour tout réel
.
Montrer que pour tout réel 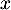 ,
, 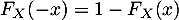 .
.
- Déterminer
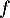 .
. 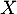 admet-elle une espérance ?
admet-elle une espérance ?
Correction
Correction
oral HEC, BL - 2022 - Exercice sans préparation.- On démontre ce résultat avec un changement de variable
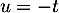 dans l'intégrale définissant la fonction de répartition et en utilisant la parité de la fonction densité
dans l'intégrale définissant la fonction de répartition et en utilisant la parité de la fonction densité 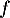 :
:
![\[\begin{array}{ll}F_X(-x)&=\dsp\int_{-\infty}^{-x}f(t)dt\\
&=\dsp\int_{+\infty}^xf(-u)(-du)\\
&=\dsp\int_x^{+\infty}f(u)du\\
&=1-F_X(x)\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/3.png)
en utilisant pour finir
![\[\int_{-\infty}^{+\infty}f(u)du=1\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/4.png)
et la relation de Chasles pour les intégrales.
- Soit la variable aléatoire
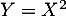 . On passe par sa fonction de répartition,
pour
. On passe par sa fonction de répartition,
pour 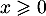 ,
,
![\[\begin{array}{ll}F_Y(x)&=P(Y\leqslant x)\\
&=P(X^2\leqslant x)\\
&=P(-\sqrt{x}\leqslant X\leqslant \sqrt{x})\\
&=F_X(\sqrt{x})-F_X(-\sqrt{x})\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/7.png)
et donc, avec le résultat de première question
![\[F_Y(x)=F_X(\sqrt{x})-\left( 1-F_X(\sqrt{x})\right)
=2F_X(\sqrt{x})-1\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/8.png)
On sait de plus que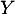 suit la loi exponentielle de param-tre
suit la loi exponentielle de param-tre 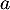 et donc que
et donc que
![\[F_Y(x)=1-e^{-ax}\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/11.png)
d'où on tire
![\[2F_X(\sqrt{x})-1=1-e^{-ax}
\iff F_X(\sqrt{x})=1-\dfrac12e^{-ax}\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/12.png)
et alors
![\[F_X(x)=1-\dfrac12e^{-ax^2}\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/13.png)
Pour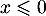 , on a
, on a
![\[F_X(x)=1-F_X(-x)=\dfrac12e^{ax^2}\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/15.png)
Pour revenir à la densité, on dérive finalement:- pour
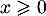 ,
, 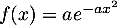
- pour
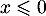 ,
, 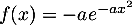
L'espérance de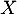 est, si elle existe,
est, si elle existe,
![\[E(X)=\int_\R xf(x)dx=\lim_{A\to+\infty}\int_{-A}^Axf(x)dx\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/21.png)
or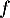 est paire, donc
est paire, donc 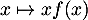 est impaire, et donc, pour tout
est impaire, et donc, pour tout 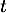 ,
,
![\[\int_{-A}^Axf(x)dx=0\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-2.2_c/25.png)
et donc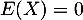 .
.
- pour
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: