Exponentielle d'une loi normale
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
On note 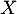 la variable aléatoire égale à la durée, en minute, d'un phénomène physique.
On note
la variable aléatoire égale à la durée, en minute, d'un phénomène physique.
On note 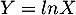 et on suppose que
et on suppose que  suit la loi
suit la loi  .
.
- Exprimer la fonction de répartition de
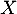 en fonction de celle de la loi de
en fonction de celle de la loi de 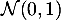 .
.
- En déduire une densité de
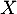 .
.
Correction
Correction
- On se ramène à la loi normale centrée réduite en posant
 telle que, donc,
telle que, donc,  .
.
On a alors la fonction de répartition de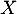 , pour
, pour  ,
,
![\[\begin{array}{ll}
F_X(x)&=P(X\leqslant x) \\
&=P\lp\ln(X)\leqslant \ln(x)\rp\\[.4em]
&=P=\left( Y\leqslant\ln(x)\rp\\[.4em]
&=P\lp\sqrt2T+1\leqslant\ln(x)\rp\\[.4em]
&=P\left( T\leqslant\dfrac{\ln(x)-1}2\rp\\[1em]
&=\Phi\lp\dfrac{\ln(x)-1}2\right)
\enar\]](/Generateur-Devoirs/Colles/VAC/exp-loi-normale_c/5.png)
avec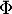 la fonction de répartition de la loi normale centrée réduite.
la fonction de répartition de la loi normale centrée réduite.
- Pour obtenir la densité, on dérive cette fonction composée.
Si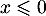 , on a
, on a 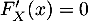 , sinon, pour
, sinon, pour 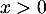 , on a
, on a
![\[F_X=\Phi(u)\]](/Generateur-Devoirs/Colles/VAC/exp-loi-normale_c/10.png)
avec , donc
, donc 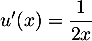 et la densité de la loi normale:
et la densité de la loi normale:
![\[\Phi'(x)=\varphi(x)=\dfrac1{\sqrt{2\pi}}e^{-\frac{x^2}2}\]](/Generateur-Devoirs/Colles/VAC/exp-loi-normale_c/13.png)
On a alors
![\[F'_X=u'\Phi'(u)\]](/Generateur-Devoirs/Colles/VAC/exp-loi-normale_c/14.png)
soit
![\[F'_X(x)=\dfrac1{2x}e^{-\frac{(ln(x)-1)^2}2}\]](/Generateur-Devoirs/Colles/VAC/exp-loi-normale_c/15.png)
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: