Sup et inf d'une loi de lois de Pareto
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit un entier naturel  , et
, et
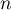 variables aléatoires indépendantes
variables aléatoires indépendantes
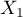 ,
, 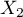 , … ,
, … , 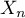 toutes de densité
toutes de densité
![\[f:\R\to\R, \, x\mapsto\la\begin{array}{cl}
0 &\text{si } x\leqslant1 \\
\dfrac1{x^2} &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto/6.png)
![\[f:\R\to\R, \, x\mapsto\la\begin{array}{cl}
0 &\text{si } x\leqslant1 \\
\dfrac1{x^2} &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto/6.png)
- Vérifier que
 est une densité de probabailité
d'une variable aléatoire.
est une densité de probabailité
d'une variable aléatoire.
- Étudier l'existence de
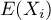 et
et 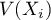 .
.
- Soit
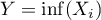 et
et
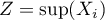 .
.
Déterminer une densité de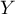 et de
et de 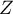 .
.
- Étudier l'existence, et calculer éventuellement la valeur,
de
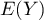 , de
, de 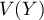 , de
, de 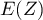 et de
et de  .
.
Correction
Correction
-
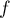 est clairement positive, continue sauf en 1, et
est clairement positive, continue sauf en 1, et
![\[\int_{-\infty}^{+\infty}f(x)dx=\int_1^{+\infty}\dfrac1{x^2}dx
=\lb-\dfrac1x\rb_1^{+\infty}=1\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/2.png)
donc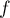 définit bien une densité de probabilité.
définit bien une densité de probabilité.
-
![\[\int_{-\infty}^{+\infty}xf(x)dx=\int_1^{+\infty}\dfrac1xdx\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/4.png)
diverge donc les variables aléatoires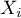 n'ont ni espérance ni variance.
n'ont ni espérance ni variance.
- On passe par la fonction de répartition: pour
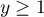 ,
,
![\[\begin{array}{ll}F_Y(y)&=P(Y\leqslant y)\\
&=1-P(Y\geqslant y)\\
&=1-P\Bigl( (X_1\geqslant y)\cap (X_2\geqslant y)\cap\dots\cap(X_n\geqslant y)\Bigr)\enar\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/7.png)
et alors, par indépendance des variables, et en posant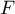 la fonction de répartition des variables
la fonction de répartition des variables 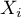 ,
,
![\[\begin{array}{ll}F_Y(y)&=1-P(X_1\geqslant y)\,P(X_\geqslant y)\,\dots\,P(X_n\geqslant y)\\
&=1-\Bigl(1-F(y)\Bigr)^n=1-\dfrac1{y^n}\enar\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/10.png)
On obtient alors la densité en dérivant
![\[f_Y(y)=\la\begin{array}{cl}0&\text{si }x\leqslant1\\
\dfrac{n}{y^{n+1}}&\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/11.png)
De même, par indépendance,
![\[\begin{array}{ll}P(Z\leq z)
&=P\Bigl(X_1\leq z)\cap (X_2\leq z)\cap\dots\cap(X_n\leq z)\Bigr)\\
&=P(X_1\leq z)\,P(X_2\leq z)\dots\,P(X_n\leq z)\\
&=\left( F(z)\rp^n=\left(1-\dfrac1z\rp^n
\enar\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/12.png)
et enfin, pour la fonction de répartition
![\[f_Z(z)=\la\begin{array}{cl}0&\text{si }x\leqslant1\\
\dfrac{n}{z^2}\lp1-\dfrac1z\rp^{n-1}&\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/13.png)
-
![\[E(Y)=n\int_1^{+\infty}\dfrac1{y^n}dy=\dfrac{n}{n-1}\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/14.png)
et
![\[E\left( Y^2\rp=n\int_1^{+\infty}\dfrac1{y^{n-1}}dy=\dfrac{n}{n-2}\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/15.png)
et donc aussi
![\[\begin{array}{ll}V(Y)
&=E\left( Y^2\rp-\left( E(Y)\rp^2\\
&=\dfrac{n}{n-2}-\dfrac{n^2}{(n-1)^2}\\
&=\dfrac{n}{(n-1)^2(n-2)}\enar\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/16.png)
Par contre,
![\[E(Z)=n\int_1^{+\infty}\dfrac1z\lp1-\dfrac1z\rp^{n-1}dz\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/17.png)
avec, en l'infini,
![\[\dfrac1z\lp1-\dfrac1z\rp^{n-1}\underset{\small+\infty}{\sim}\dfrac1z\]](/Generateur-Devoirs/Colles/VAC/sup-inf-pareto_c/18.png)
et donc l'intégrale diverge: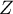 n'admet pas d'espérance et donc ni de variance.
n'admet pas d'espérance et donc ni de variance.
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: