Somme de 2 lois de Poisson
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires discrètesVariables aléatoires discrètes
Énoncé du sujet
Soit 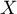 et
et 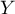 deux variables aléatoires indépendantes suivant
des lois de Poisson de paramètre respectif
deux variables aléatoires indépendantes suivant
des lois de Poisson de paramètre respectif 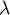 et
et 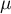 .
.
Démontrer que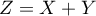 suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre 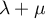 .
.
Démontrer que
Correction
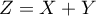 ,
c'est-à-dire les probabilités
,
c'est-à-dire les probabilités
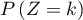 pour tout entier
pour tout entier 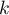 .
.
L'événement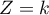 est la réunion disjointe des événements
est la réunion disjointe des événements
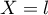 et
et 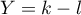 pour
pour 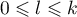 .
.
On a donc, par indépendance des variables aléatoires,
![\[\begin{array}{lcl}
P(Z=k)&=&\dsp\sum_{l=0}^k P\Bigl(\left( X=l\rp\cap\left( Y=k-l\rp\Bigr)\\[1.2em]
&=&\dsp\sum_{l=0}^k P(X=l)\,P(Y=k-l)\\[1.2em]
&=&\dsp\sum_{l=0}^k e^{-\lambda}\frac{\lambda^l}{l!}e^{-\mu}\frac{\mu^{k-l}}{(k-l)!}\\[1.2em]
&=&e^{-(\lambda+\mu)}\dsp\sum_{l=0}^k \dfrac1{l!(k-l)!}\lambda^l\mu^{k-l}
\enar\]](/Generateur-Devoirs/Colles/VAD/SommeLoisPoisson_c/8.png)
On voit alors apparaître la formule du binôme de Newton de
![\[(\lambda+\mu)^k=\sum_{l=0}^k \binom kl \lambda^l \mu^{k-l}\]](/Generateur-Devoirs/Colles/VAD/SommeLoisPoisson_c/9.png)
avec les coefficients binomiaux
![\[\binom kl=\dfrac{k!}{l!(k-l)!}\]](/Generateur-Devoirs/Colles/VAD/SommeLoisPoisson_c/10.png)
et on a donc alors
![\[\begin{array}{lcl}P(Z=k)=
&=&\dsp\dfrac{e^{-(\lambda+\mu)}}{k!}\sum_{l=0}^k \binom kl \lambda^l \mu^{k-l}\\[1.2em]
&=&\dfrac{e^{-(\lambda+\mu)}}{k!}(\lambda+\mu)^k\enar\]](/Generateur-Devoirs/Colles/VAD/SommeLoisPoisson_c/11.png)
ce qui montre que la variable aléatoire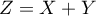 suit bien
une loi de Poisson de paramètre
suit bien
une loi de Poisson de paramètre 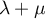 .
.
Correction
On cherche à déterminer la loi de probabilité deL'événement
On a donc, par indépendance des variables aléatoires,
![\[\begin{array}{lcl}
P(Z=k)&=&\dsp\sum_{l=0}^k P\Bigl(\left( X=l\rp\cap\left( Y=k-l\rp\Bigr)\\[1.2em]
&=&\dsp\sum_{l=0}^k P(X=l)\,P(Y=k-l)\\[1.2em]
&=&\dsp\sum_{l=0}^k e^{-\lambda}\frac{\lambda^l}{l!}e^{-\mu}\frac{\mu^{k-l}}{(k-l)!}\\[1.2em]
&=&e^{-(\lambda+\mu)}\dsp\sum_{l=0}^k \dfrac1{l!(k-l)!}\lambda^l\mu^{k-l}
\enar\]](/Generateur-Devoirs/Colles/VAD/SommeLoisPoisson_c/8.png)
On voit alors apparaître la formule du binôme de Newton de
![\[(\lambda+\mu)^k=\sum_{l=0}^k \binom kl \lambda^l \mu^{k-l}\]](/Generateur-Devoirs/Colles/VAD/SommeLoisPoisson_c/9.png)
avec les coefficients binomiaux
et on a donc alors
![\[\begin{array}{lcl}P(Z=k)=
&=&\dsp\dfrac{e^{-(\lambda+\mu)}}{k!}\sum_{l=0}^k \binom kl \lambda^l \mu^{k-l}\\[1.2em]
&=&\dfrac{e^{-(\lambda+\mu)}}{k!}(\lambda+\mu)^k\enar\]](/Generateur-Devoirs/Colles/VAD/SommeLoisPoisson_c/11.png)
ce qui montre que la variable aléatoire
Tag:Variables aléatoires discrètes
Autres sujets au hasard:

Voir aussi: