Loi géométrique est sans mémoire
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires discrètesVariables aléatoires discrètes
Énoncé du sujet
Une variable aléatoire discrète à valeurs dans 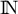 est dite
sans mémoire si, pour tous
est dite
sans mémoire si, pour tous 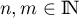 ,
,
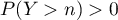 et
et
![\[P_{(Y>n)}(Y>n+m)=P(Y>m)\]](/Generateur-Devoirs/Colles/VAD/GeomSansMemoire/4.png)
Montrer que si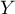 suit une loi géométrique alors
suit une loi géométrique alors 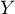 est sans mémoire.
est sans mémoire.
Interpréter ce résultat en considérant une suite d'épreuves répétées.
Montrer que si
Interpréter ce résultat en considérant une suite d'épreuves répétées.
Correction
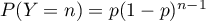 et
donc (c'est aussi du cours, mais il faut savoir le (re)démontrer)
et
donc (c'est aussi du cours, mais il faut savoir le (re)démontrer)
![\[\begin{array}{ll}
P(Y>n)&=\dsp\sum_{k>n}p(1-p)^{k-1}\\
&=p(1-p)^n\dsp\sum_{k=0}^{+\infty}(1-p)^k\\
&=p(1-p)^n\dfrac1{1-(1-p)}\\[1em]
&=(1-p)^n\enar\]](/Generateur-Devoirs/Colles/VAD/GeomSansMemoire_c/2.png)
et alors,
![\[\begin{array}{ll}P_{(Y>n)}(Y>n+m)
&=\dfrac{P\Bigl( \left( Y>n+m\rp\cap\left( Y>n\rp\Bigr)}{P\left( Y>n\rp}\\[1.2em]
&=\dfrac{P\left( Y>n+m\right)}{P\left( Y>n\right)}\\[1.2em]
&=\dfrac{(1-p)^{n+m}}{(1-p)^n}\\[1em]
&=(1-p)^m\\[.8em]
&=P(Y>m)\enar\]](/Generateur-Devoirs/Colles/VAD/GeomSansMemoire_c/3.png)
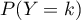 est la probabilité d'obtenir le premier succès au k-ième essai
lors de la répétition d'épreuves de Bernoulli.
est la probabilité d'obtenir le premier succès au k-ième essai
lors de la répétition d'épreuves de Bernoulli.
Cette propriété "sans mémoire" s'interprète alors par: après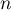 essais infructueux, la probabilité d'attendre
essais infructueux, la probabilité d'attendre 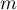 essais
suplémentaires pour obtenir le 1er succès (et donc d'obtenir le 1er succès au bout de
essais
suplémentaires pour obtenir le 1er succès (et donc d'obtenir le 1er succès au bout de  essais), est la même que d'obtenir tout simplement le 1er succès après
essais), est la même que d'obtenir tout simplement le 1er succès après 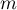 essais.
essais.
En d'autres termes, de savoir qu'après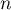 essais on n'a pas eu de succès n'apporte aucune information: on oublie tout simplement ces résultats et tout se psse comme si on repartait de 0.
essais on n'a pas eu de succès n'apporte aucune information: on oublie tout simplement ces résultats et tout se psse comme si on repartait de 0.
Correction
On a![\[\begin{array}{ll}
P(Y>n)&=\dsp\sum_{k>n}p(1-p)^{k-1}\\
&=p(1-p)^n\dsp\sum_{k=0}^{+\infty}(1-p)^k\\
&=p(1-p)^n\dfrac1{1-(1-p)}\\[1em]
&=(1-p)^n\enar\]](/Generateur-Devoirs/Colles/VAD/GeomSansMemoire_c/2.png)
et alors,
![\[\begin{array}{ll}P_{(Y>n)}(Y>n+m)
&=\dfrac{P\Bigl( \left( Y>n+m\rp\cap\left( Y>n\rp\Bigr)}{P\left( Y>n\rp}\\[1.2em]
&=\dfrac{P\left( Y>n+m\right)}{P\left( Y>n\right)}\\[1.2em]
&=\dfrac{(1-p)^{n+m}}{(1-p)^n}\\[1em]
&=(1-p)^m\\[.8em]
&=P(Y>m)\enar\]](/Generateur-Devoirs/Colles/VAD/GeomSansMemoire_c/3.png)
Cette propriété "sans mémoire" s'interprète alors par: après
En d'autres termes, de savoir qu'après
Tag:Variables aléatoires discrètes
Autres sujets au hasard:

Voir aussi: