Série géométrique dérivée, loi du 1er succès et loi du nombre de succès avec des cartes
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires discrètesVariables aléatoires discrètes
Énoncé du sujet
- Exprimer la somme de la série
 .
.
- Je tire une carte dans un jeu de 32 cartes:
si c'est un as j'ai gagné, sinon je replace la carte et je recommence.
On note
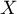 la variable aléatoire égale au nombre de tirages effectués
avant de gagner.
Exprimer
la variable aléatoire égale au nombre de tirages effectués
avant de gagner.
Exprimer 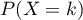 pour
pour 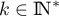 .
.
Combien de cartes vais-je tirer en moyenne. - Je tire successivement 10 cartes comme précédemment,
en les remettant à chaque fois dans le paquet, et
indépendamment de la carte tirée (as ou non).
On note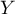 la variable aléatoire égale au nombre d'as tirés.
Quelle est la loi de probabilité de
la variable aléatoire égale au nombre d'as tirés.
Quelle est la loi de probabilité de 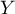 ?
Combien d'as vais-je tirer en moyenne ?
?
Combien d'as vais-je tirer en moyenne ?
Correction
Correction
- Pour
 , on pose
qui est une série absolument convergente. On a aussi
, on pose
qui est une série absolument convergente. On a aussi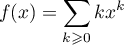 avec
avec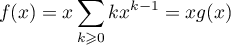
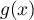 qui est la dérivée d'une somme géométrique.
qui est la dérivée d'une somme géométrique.
Plus précisément, on a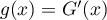 avec
avec
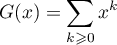 .
.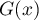 est une série géométrique,
est une série géométrique,
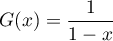 et donc
et donc 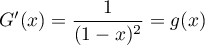 .
On trouve ainsi,
.
On trouve ainsi,
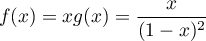 .
.
- La probabilité de tirer un as est
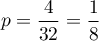 .
.
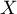 est égale au rang du 1er succès:
est égale au rang du 1er succès:
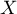 suit donc la loi géométrique de paramètre
suit donc la loi géométrique de paramètre 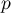 et alors
et alors
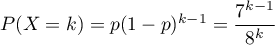 .
Le nombre de cartes tirées en moyenne est l'espérance de
.
Le nombre de cartes tirées en moyenne est l'espérance de 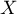 ,
soit
,
soit
![\[E(X)=\sum_{k>0}kP(X=k)
=\sum_{k>0}kp(1-p)^{k-1}\]](/Generateur-Devoirs/Colles/VAD/CoursLoiGeomBinom_c/17.png)
soit, en utilisant la question précédente avec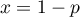 ,
,
![\[\begin{array}{ll}
E(X)&=\dfrac{p}{1-p}\dsp\sum_{k>0}k(1-p)^k\\
&=\dfrac{p}{1-p}\tm\dfrac{1-p}{\lp1-(1-p)\rp^2}\\[1em]
&=\dfrac1p\enar\]](/Generateur-Devoirs/Colles/VAD/CoursLoiGeomBinom_c/19.png)
Ici, avec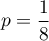 , et on a donc
, et on a donc 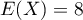 :
en moyenne il faut tirer 8 cartes pour tomber sur un as.
:
en moyenne il faut tirer 8 cartes pour tomber sur un as.
-
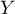 est égale au nombre de succès sur les 10 tirages:
est égale au nombre de succès sur les 10 tirages:
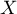 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres  et
et 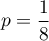 .
La probabilité de tirer 2 as est donc
.
La probabilité de tirer 2 as est donc
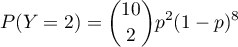 .
Le nombre d'as tirés en moyenne est l'espérance:
.
Le nombre d'as tirés en moyenne est l'espérance:
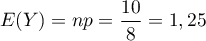 as tirés en moyenne toutes les 10 cartes.
as tirés en moyenne toutes les 10 cartes.
Tag:Variables aléatoires discrètes
Autres sujets au hasard:

Voir aussi: