Variation et maximum d'une loi de Poisson

Colle de mathématiques

Sujet de colle de maths:

Soit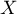

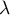une variable aléatoire suivant la loi de Poisson de paramètre $\lambda$ . On note

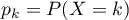Déterminer une condition nécessaire et suffisante sur 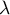$\lambda$ pour que la suite 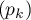soit décroissante.
Quel est le maximum de la suite ?

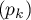Cor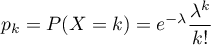rection

On a $p_k=P(X=k)=e^{-\lambda}\dfrac{\lambda^k}{k!}$ .

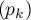est décroissante si et seulement si 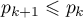$p_{k+1}\leqslant p_k$ pour tout .
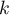Or,

$\begin{array}{ll} p_{k+1}\leqslant p_k &\iff e^{-\lambda}\dfrac{\lambda^{k+1}}{(k+1)!} < e^{-\lambda}\dfrac{\lambda^k}{k!} \\[1em] &\iff \dfrac{\lambda}{k+1}<1\\[1.2em] &\iff \lambda<k+1 \enar$

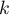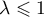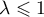Cette inégalité doit être vraie pour tout entier ; on doit donc avoir $\lambda\leqslant1$ . La suite est donc décroissante lorsque $\lambda\leqslant1$ .
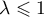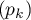D'après le résultat précédent, si $\lambda\leqslant1$ , la suite $\left( p_k\rp$ est monotone et décroissante. Son maximum est donc .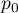
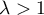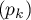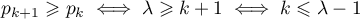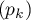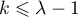Maintenant, si $\lambda>1$ , $\left( p_k\rp$ est croissante jusqu'à un certain rang, qu'il s'agit de déterminer. Toujours d'après le calcul précédent, on a $p_{k+1}\geqslant p_k \iff \lambda\geqslant k+1 \iff k\leqslant\lambda-1$ et la suite $\left( p_k\rp$ est donc croissante tant que $k\leqslant\lambda-1$ .
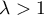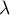Pour $\lambda>1$ , le maximum est donc atteint en la partie entière de $\lambda$ .

Autres sujets au hasard: