Résolution d'un système 3x3 par le pivot de Gauss-Jordan
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
Énoncé du sujet
En utilisant l'algorithme du pivot de Gauss-Jordan, résoudre le système
![\[\la\begin{array}{rcrcrcc}
3x&+&y&-&z &=&4\\
2x&-&y&+&z &=&6\\
-x&-&y&+&2z &=&6
\enar\right.\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2/1.png)
![\[\la\begin{array}{rcrcrcc}
3x&+&y&-&z &=&4\\
2x&-&y&+&z &=&6\\
-x&-&y&+&2z &=&6
\enar\right.\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2/1.png)
Correction
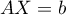 avec
avec
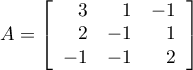 ,
,
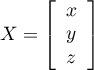 et
et
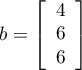 .
.
Pour utiliser la méthode du pivot de Gauss-Jordan, on écrit ensuite la matrice augmentée
![\[\lb\begin{array}{rrr|r}3&1&-1&4\\2&-1&1&6\\-1&-1&2&6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/5.png)
On ramène le pivot de la 1ère ligne à 1 par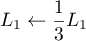 ,
,
![\[\lb\begin{array}{rrr|r}1&\dfrac13&-\dfrac13 &\dfrac43\\[.6em]
2&-1&1&6\\-1&-1&2&6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/7.png)
puis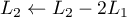 et
et 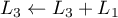 pour obtenir
pour obtenir
![\[\lb\begin{array}{rrr|r}1&\dfrac13&-\dfrac13 &\dfrac43\\[.6em]
0&-\dfrac53&\dfrac53&\dfrac{10}3\\[.6em]
0&-\dfrac23&\dfrac53&\dfrac{22}3\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/10.png)
on ramène le pivot de la deuxième ligne à 1 par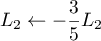
![\[\lb\begin{array}{rrr|r}1&\dfrac13&-\dfrac13 &\dfrac43\\[.6em]
0&1&-1&-2\\[.6em]
0&-\dfrac23&\dfrac53&\dfrac{22}3\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/12.png)
puis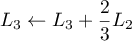 et
et 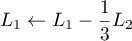 pour obtenir
pour obtenir
![\[\lb\begin{array}{rrr|r}
1&0&0 &2\\[.8em]
0&1&-1 &-2\\[.8em]
0&0&1 &6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/15.png)
enfin,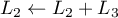 donne
donne
![\[\lb\begin{array}{rrr|r}
1&0&0 &2\\[.8em]
0&1&0 &4\\[.8em]
0&0&1 &6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/17.png)
et on trouve donc ici la solution![$X=\lb\begin{array}{c}x\\y\\z\enar\right]
=
\lb\begin{array}{c}2\\4\\6\enar\rb$](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/18.png)
Correction
On écrit le système sous forme matricielle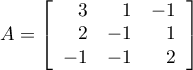 ,
,
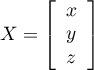 et
et
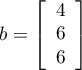 .
.
Pour utiliser la méthode du pivot de Gauss-Jordan, on écrit ensuite la matrice augmentée
![\[\lb\begin{array}{rrr|r}3&1&-1&4\\2&-1&1&6\\-1&-1&2&6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/5.png)
On ramène le pivot de la 1ère ligne à 1 par
![\[\lb\begin{array}{rrr|r}1&\dfrac13&-\dfrac13 &\dfrac43\\[.6em]
2&-1&1&6\\-1&-1&2&6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/7.png)
puis
![\[\lb\begin{array}{rrr|r}1&\dfrac13&-\dfrac13 &\dfrac43\\[.6em]
0&-\dfrac53&\dfrac53&\dfrac{10}3\\[.6em]
0&-\dfrac23&\dfrac53&\dfrac{22}3\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/10.png)
on ramène le pivot de la deuxième ligne à 1 par
![\[\lb\begin{array}{rrr|r}1&\dfrac13&-\dfrac13 &\dfrac43\\[.6em]
0&1&-1&-2\\[.6em]
0&-\dfrac23&\dfrac53&\dfrac{22}3\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/12.png)
puis
![\[\lb\begin{array}{rrr|r}
1&0&0 &2\\[.8em]
0&1&-1 &-2\\[.8em]
0&0&1 &6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/15.png)
enfin,
![\[\lb\begin{array}{rrr|r}
1&0&0 &2\\[.8em]
0&1&0 &4\\[.8em]
0&0&1 &6\enar\rb\]](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/17.png)
et on trouve donc ici la solution
![$X=\lb\begin{array}{c}x\\y\\z\enar\right]
=
\lb\begin{array}{c}2\\4\\6\enar\rb$](/Generateur-Devoirs/Colles/matrices/systeme-GJ-2_c/18.png)
Tag:Matrices
Autres sujets au hasard:
