Calcul matriciel - Inverse d'une matrice 4x4

Colle de mathématiques

Sujet de colle de maths:

On considère la matrice carrée $K=\lp\begin{array}{cccc}1&1&-1&-3\\1&1&1&-2\\0&-1&0&1\\1&1&0&-2\enar\rp$ .

Calculer .
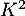En déduit que 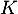est inversible et calculer $K^{-1}$ .
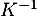Soit et 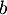deux réels. On définit la matrice 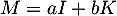. Montrer que .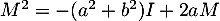
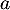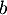En déduire que si et ne sont pas tous les deux nuls, 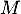est inversible.
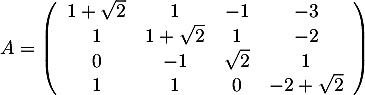En déduire l'inverse de la matrice $A=\lp\begin{array}{cccc}1+\sqrt2&1&-1&-3\\1&1+\sqrt2&1&-2\\0&-1&\sqrt2&1\\1&1&0&-2+\sqrt2\enar\rp$ .

Correction

$\begin{array}{ll}K^2&=\lp\begin{array}{cccc}1&1&-1&-3\\1&1&1&-2\\0&-1&0&1\\1&1&0&-2\enar\rp\lp\begin{array}{cccc}1&1&-1&-3\\1&1&1&-2\\0&-1&0&1\\1&1&0&-2\enar\rp\\[2.4em] &=\lp\begin{array}{cccc}-1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\enar\rp\enar$

c'est-à-dire que .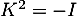
On en déduit que 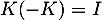et donc que 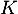est inversible avec $K^{-1}=-K$ .
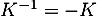On a, puisque l'identité 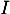commutent avec toutes les matrices, donc avec ,

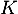$\begin{array}{ll}M^2&=\left( aI+bK\rp^2\\[.4em] &=a^2I^2+2abIK+b^2K^2\\[.4em] &=a^2I+2abK+b^2K^2\enar$

Soit, avec le résultat de la question précédente,

$M^2=a^2I+2abK-b^2I$

ou encore, puisque ,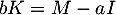

$\begin{array}{ll}M^2&=a^2I+2a(M-aI)-b^2I\\[.4em]&=-(a^2+b^2)I+2aM\enar$
On en déduit que

$M^2-2aM=-(a^2+b^2)I$

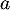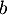et donc, si et ne sont pas tous les deux nuls, donc si 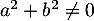$a^2+b^2\not=0$ , alors

$\dfrac{-1}{a^2+b^2}(M-2aI)M=I$

ce qui montre que la matrice est alors inversible, d'inverse

$M^{-1}=\dfrac{-1}{a^2+b^2}(M-2aI)$
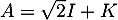On a $A=\sqrt2I+K$ , et donc, avec 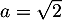$a=\sqrt2$ et 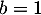, on trouve l'inverse

$A^{-1}=\dfrac{-1}{\sqrt2^2+1^2}(A-2\sqrt2I)$

soit

$A^{-1}=\dfrac{-1}3 \lp\begin{array}{cccc}1-\sqrt2&1&-1&-3\\1&1-\sqrt2&1&-2\\0&-1&-\sqrt2&1\\1&1&0&-2-\sqrt2\enar\rp$

Tag:Matrices

Autres sujets au hasard:

Voir aussi: