Calcul matriciel - Sous espace vectoriel de matrices
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
- Espace vectorielEspaces vectoriels
Énoncé du sujet
On consdière les matrices
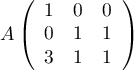 ,
,
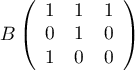 ,
,
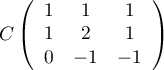 .
.
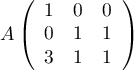 ,
,
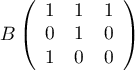 ,
,
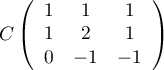 .
.
- Calculer
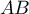 et
et 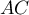 .
.
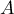 peut-elle être inversible ?
peut-elle être inversible ?
- Déterminer l'ensemble
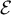 des matrices
des matrices 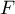 vérifiant
vérifiant 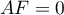 .
.
Montrer que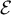 est un sous espace vectoriel et préciser sa dimension.
est un sous espace vectoriel et préciser sa dimension.
Correction
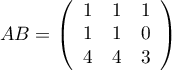 ,
et de même
,
et de même
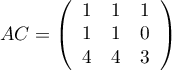 .
.
On a donc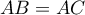 , ou encore
, ou encore 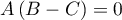 .
Ceci montre en particulier que
.
Ceci montre en particulier que 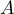 ne peut pas être inversible.
ne peut pas être inversible.
On peut aussi interpréter en considérant l'application linéaire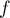 dont la matrice (dans la base canonique par exemple) est
dont la matrice (dans la base canonique par exemple) est 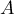 .
Alors
.
Alors 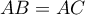 montre directement que
montre directement que 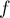 n'est pas injective et donc ne peut bijective: sa matrice n'est pas inversible.
n'est pas injective et donc ne peut bijective: sa matrice n'est pas inversible.
L'ensemble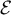 est clairement un sous espace vectoriel: c'est le noyau de l'application linéaire "produit à droite":
est clairement un sous espace vectoriel: c'est le noyau de l'application linéaire "produit à droite": 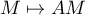 .
.
Soit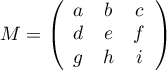 une matrice quelconque,
alors
une matrice quelconque,
alors
![\[\begin{array}{ll}AM=0&\iff\la\begin{array}{l}a=b=c=0\\d+g=e+h=f+i=0\\3a+d+g=3b+e+h=3c+f+i=0\enar\right.\\[2em]
&\iff\la\begin{array}{l}a=b=c=0\\d+g=e+h=f+i=0\enar\right.\enar\]](/Generateur-Devoirs/Colles/matrices/exssevmat_c/13.png)
Ce qui montre que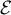 est généré par les trosi matrices,
est généré par les trosi matrices,
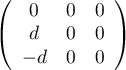 ,
,
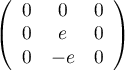 , et
, et
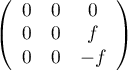 , ou encore que
, ou encore que
![\[\mathcal E=\text{Vect}\left\{
M_1=\lp\begin{array}{ccc}0&0&0\\1&0&0\\-1&0&0\enar\rp,
M_2=\lp\begin{array}{ccc}0&0&0\\0&1&0\\0&-1&0\enar\rp,
M_3=\lp\begin{array}{ccc}0&0&0\\0&0&1\\0&0&-1\enar\rp\right\}\]](/Generateur-Devoirs/Colles/matrices/exssevmat_c/18.png)
On a alors aussi trouvé que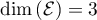 .
.
Correction
On calcule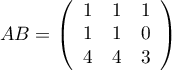 ,
et de même
,
et de même
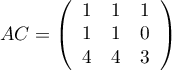 .
.
On a donc
On peut aussi interpréter en considérant l'application linéaire
L'ensemble
Soit
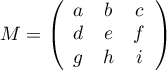 une matrice quelconque,
alors
une matrice quelconque,
alors
![\[\begin{array}{ll}AM=0&\iff\la\begin{array}{l}a=b=c=0\\d+g=e+h=f+i=0\\3a+d+g=3b+e+h=3c+f+i=0\enar\right.\\[2em]
&\iff\la\begin{array}{l}a=b=c=0\\d+g=e+h=f+i=0\enar\right.\enar\]](/Generateur-Devoirs/Colles/matrices/exssevmat_c/13.png)
Ce qui montre que
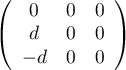 ,
,
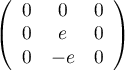 , et
, et
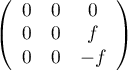 , ou encore que
, ou encore que
![\[\mathcal E=\text{Vect}\left\{
M_1=\lp\begin{array}{ccc}0&0&0\\1&0&0\\-1&0&0\enar\rp,
M_2=\lp\begin{array}{ccc}0&0&0\\0&1&0\\0&-1&0\enar\rp,
M_3=\lp\begin{array}{ccc}0&0&0\\0&0&1\\0&0&-1\enar\rp\right\}\]](/Generateur-Devoirs/Colles/matrices/exssevmat_c/18.png)
On a alors aussi trouvé que
Tags:MatricesEspace vectoriel
Autres sujets au hasard:

Voir aussi: