Minorer un produit
Colle de mathématiques
Sujet de colle de maths:- SommesSommes des termes d'une suite
- RécurrenceDémonstration par récuurrence
Énoncé du sujet
Démontrer l'inégalité, pour tout 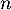 entier naturel,
entier naturel,
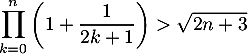
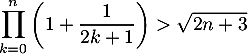
Correction
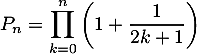 , et on cherche alors à démontrer que
, et on cherche alors à démontrer que
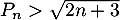 .
.
On peut démontrer cette inégalité par récurrence.
Initialisation: Pour , on
, on 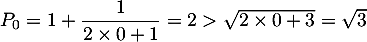 .
.
L'inégalité est donc bien vraie initialement.
Hérédité: Supposons que, pour un certain entier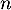 , on ait
, on ait 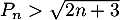 .
.
Au rang suivant, on a alors
![\[\begin{array}{ll}P_{n+1}&=\dsp\prod_{k=0}^{n+1}\lp1+\dfrac1{2k+1}\rp\\
&=\dsp\lp\prod_{k=0}^n\lp1+\dfrac1{2k+1}\rp\rp\lp1+\dfrac1{2(n+1)+1}\rp\\
&=P_n\lp1+\dfrac1{2n+3}\right)
\enar\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/7.png)
On a alors, en utilisant l'hypothèse de récurrence
![\[P_{n+1}>\sqrt{2n+3}\lp1+\dfrac1{2n+3}\rp\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/8.png)
Or
![\[\sqrt{2n+3}\lp1+\dfrac1{2n+3}\rp=\sqrt{2n+3}\dfrac{2n+4}{2n+3}
=\dfrac{2n+4}{\sqrt{2n+3}}\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/9.png)
On cherche donc maintenant à montrer que
![\[\dfrac{2n+4}{\sqrt{2n+3}}>\sqrt{2n+5}\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/10.png)
soit aussi, en élevant au carré puisque tous les termes sont strictement positifs,
![\[(2n+4)^2>(2n+3)(2n+5)\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/11.png)
Cette dernière inégalité est toujours vraie car en développant elle est équivalente à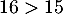 , et ainsi, on a bien
, et ainsi, on a bien
![\[\begin{array}{lll}&(2n+4)^2&>(2n+3)(2n+5)\\[.5em]
\iff &(2n+4)&>\sqrt{(2n+3)(2n+5)}\\[.5em]
\iff &\dfrac{2n+4}{\sqrt{2n+3}}&>\sqrt{2n+5}\end{array}
\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/13.png)
et donc finalement
![\[P_{n+1}>\sqrt{2n+5}\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/14.png)
ce qui montre l'hérédité de notre propriété, c'est-à-dire que la propriété est encore vraie au rang suivant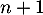 .
.
Conclusion: On vient donc finalement de démontrer que l'inégalité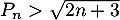 est vraie pour tout entier
est vraie pour tout entier 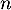 .
.
Correction
On note le produit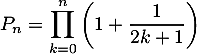 , et on cherche alors à démontrer que
, et on cherche alors à démontrer que
On peut démontrer cette inégalité par récurrence.
Initialisation: Pour
L'inégalité est donc bien vraie initialement.
Hérédité: Supposons que, pour un certain entier
Au rang suivant, on a alors
![\[\begin{array}{ll}P_{n+1}&=\dsp\prod_{k=0}^{n+1}\lp1+\dfrac1{2k+1}\rp\\
&=\dsp\lp\prod_{k=0}^n\lp1+\dfrac1{2k+1}\rp\rp\lp1+\dfrac1{2(n+1)+1}\rp\\
&=P_n\lp1+\dfrac1{2n+3}\right)
\enar\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/7.png)
On a alors, en utilisant l'hypothèse de récurrence
Or
On cherche donc maintenant à montrer que
soit aussi, en élevant au carré puisque tous les termes sont strictement positifs,
Cette dernière inégalité est toujours vraie car en développant elle est équivalente à
![\[\begin{array}{lll}&(2n+4)^2&>(2n+3)(2n+5)\\[.5em]
\iff &(2n+4)&>\sqrt{(2n+3)(2n+5)}\\[.5em]
\iff &\dfrac{2n+4}{\sqrt{2n+3}}&>\sqrt{2n+5}\end{array}
\]](/Generateur-Devoirs/Colles/Suites/Produit-Recurrence_c/13.png)
et donc finalement
ce qui montre l'hérédité de notre propriété, c'est-à-dire que la propriété est encore vraie au rang suivant
Conclusion: On vient donc finalement de démontrer que l'inégalité
Tags:SommesRécurrence
Autres sujets au hasard:

Voir aussi: