Calcul d'une somme
Colle de mathématiques
Sujet de colle de maths:- SommesSommes des termes d'une suite
Énoncé du sujet
On pose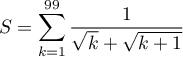 
.
Montrer que, pour tout entier naturel non nul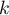
,
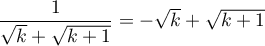et calculer la valeur exacte de 
.
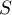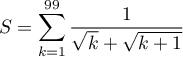. Montrer que, pour tout entier naturel non nul
,
et calculer la valeur exacte de .
Correction
,
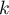![\[\begin{array}{ll}\dfrac{1}{\sqrt{k}+\sqrt{k+1}}\tm\dfrac{-\sqrt{k}+\sqrt{k+1}}{-\sqrt{k}+\sqrt{k+1}}
&=\dfrac{-\sqrt{k}+\sqrt{k+1}}{-k+(k+1)}\\[.8em]
&=-\sqrt{k}+\sqrt{k+1}\enar\]](/Generateur-Devoirs/Colles/Suites/exSomme_c/2.png)
On a alors,
![\[\begin{array}{ll}S&=\dsp\sum_{k=1}^{99}\dfrac{1}{\sqrt{k}+\sqrt{k+1}}\\[1em]
&=\dsp\sum_{k=1}^{99}-\sqrt{k}+\sqrt{k+1} \\[.5em]
&=\dsp-\sum_{k=1}^{99}\sqrt{k}+\sum_{k=1}^{99}\sqrt{k+1} \\[.5em]
&=\dsp-\sum_{k=1}^{99}\sqrt{k}+\sum_{k=2}^{100}\sqrt{k} \\[.5em]
&=-\sqrt1+\sqrt{100}=9\enar\]](/Generateur-Devoirs/Colles/Suites/exSomme_c/3.png)
Correction
Pour tout entier naturel non nul,
On a alors,
Tag:Sommes
Autres sujets au hasard:
Voir aussi: