Matrice imaginaire
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
- Espace vectorielEspaces vectoriels
- Applications linéairesApplications linéaires
Énoncé du sujet
Pour un entier 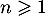 , on note
, on note 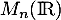 l'ensemble des matrices à
l'ensemble des matrices à 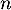 lignes,
lignes, 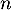 colonnes et à coefficients réels.
On note
colonnes et à coefficients réels.
On note 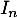 la matrice identité de
la matrice identité de 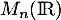 .
.
Soit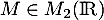 une matrice telle que
une matrice telle que 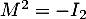 .
.
Soit
- La matrice
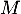 possède-t-elle des valeurs propres ?
possède-t-elle des valeurs propres ?
- Quel est le rang de
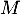 ?
?
- Soit
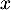 un vecteur non nul et
un vecteur non nul et 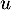 l'endomorphisme de
l'endomorphisme de 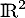 canoniquement associé à
canoniquement associé à  .
.
Montrer que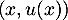 est une base de
est une base de 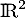 et donner la matrice de
et donner la matrice de 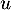 dans cette base.
dans cette base.
- Trouver toutes les matrices
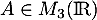 telles que
telles que 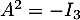 .
.
Correction
Correction
Oral ENS ULM - 2021- Soit
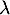 une valeur propre de
une valeur propre de 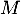 , alors il existe un vecteur non nul
, alors il existe un vecteur non nul 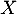 tel que
tel que 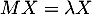 .
.
En multipliant par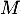 , on a alors,
, on a alors, 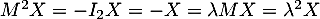 ,
et donc, nécessairement
,
et donc, nécessairement 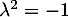 car
car 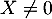 .
.
C'est impossible (dans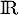 ), et donc
), et donc 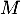 n'a pas de valeur propre.
n'a pas de valeur propre.
- Comme
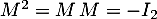 , on a aussi
, on a aussi 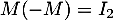 , ce qui montre
, ce qui montre 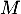 est inversible (d'inverse
est inversible (d'inverse 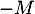 ), et en particulier que
), et en particulier que 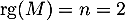 .
.
On aurait aussi pu s'intéresser au noyau: soit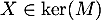 , alors
, alors
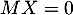 donc
donc 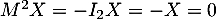 , d'où
, d'où 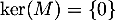 , et on arrive à la même conclusion.
, et on arrive à la même conclusion.
- Comme on a deux vecteurs dans un espace de dimension 2, il suffit de montrer que cette famille est libre.
Soit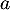 et
et 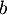 avec
avec 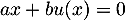 , alors,
en appliquant
, alors,
en appliquant 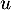 on obtient
on obtient
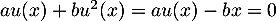 , d'où le système
, d'où le système
![\[\la\begin{array}{rcrcl}
ax&+&bu(x)&=&0\\
-bx&+&au(x)&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/matrices/Mi_c/25.png)
Si , la deuxième équation donne aussi
, la deuxième équation donne aussi 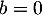 , car
, car 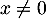 .
.
Si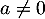 , la combinaison
, la combinaison 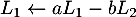 donne
donne
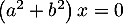 soit
soit 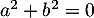 , car
, car 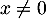 ,
et donc
,
et donc 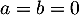 : la famille est libre et forme donc une base de
: la famille est libre et forme donc une base de  .
.
Dans cette base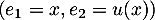 , on a
, on a
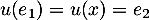 et
et 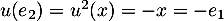 ,
d'où la matrice dans cette base
,
d'où la matrice dans cette base
![\[\lp\begin{array}{cc}0&-1\\1&0\enar\rp\]](/Generateur-Devoirs/Colles/matrices/Mi_c/39.png)
- En raisonnant comme précédemment, une telle matrice n'admet pas de valeur propre, est de rang 3 (c'est-à-dire inversible), et si
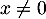 , alors
, alors
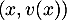 est une famille libre (avec
est une famille libre (avec 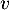 l'endomorphisme canoniquement associé).
l'endomorphisme canoniquement associé).
On complète cette base pour en obtenir une de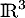 , et dans celle-ci,
la matrice s'écrit
, et dans celle-ci,
la matrice s'écrit
![\[A'=\lp\begin{array}{ccc}0&-1&\alpha\\1&0&\beta\\0&0&\gamma\enar\rp\]](/Generateur-Devoirs/Colles/matrices/Mi_c/44.png)
Maintenant,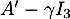 n'est pas inversible, c'est-à-dire que
n'est pas inversible, c'est-à-dire que
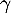 est une valeur propre de
est une valeur propre de 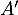 , donc de
, donc de 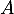 , ce qui est impossible.
, ce qui est impossible.
On en conclut qu'il n'existe pas de telle matrice.
Remarque: sans revenir aux valeurs propres, une fois qu'on a obtenu la forme nécéssaire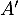 pour de telles matrices, il suffit de calculer
pour de telles matrices, il suffit de calculer
![\[A'^2=\lp\begin{array}{ccc}-1&0&\dots\\0&-1&\dots\\0&0&\gamma^2\enar\rp\]](/Generateur-Devoirs/Colles/matrices/Mi_c/50.png)
et donc pour avoir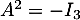 , il faut nécessairement avoir
, il faut nécessairement avoir 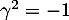 , ce qui est impossible.
, ce qui est impossible.
Tags:MatricesEspace vectorielApplications linéaires
Autres sujets au hasard:
