Famille libre ?
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
- DéterminantsDéterminants de matrices
Énoncé du sujet
À quelle condition sur le réel  ,
la famille
,
la famille  , avec
, avec
![\[ e_1=(a;1;1)\ ,\ e_2=(1;a;1)\ ,\ e_3=(1;1;a)\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre/3.png)
est-elle une base de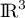 ?
?
est-elle une base de
Correction
![\[D(a)=\left|\begin{array}{ccc}a&1&1\\1&a&1\\1&1&a\enar\right|\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre_c/1.png)
La famille est libre, donc une base, si et seulement si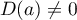 .
.
En ajjoutant les 3 colonnes dans la 1ère, on obtient,
![\[D(a)=\left|\begin{array}{ccc}2+a&1&1\\2+a&a&1\\2+a&1&a\enar\right|
=(2+a)\left|\begin{array}{ccc}1&1&1\\1&a&1\\1&1&a\enar\right|\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre_c/3.png)
puis en soustrayant la 2ème colonne à la 1ère,
![\[D(a)=(2+a)\left|\begin{array}{ccc}0&1&1\\1-a&a&1\\0&1&a\enar\right|
=-(2+a)(1-a)\left|\begin{array}{cc}1&1\\1&a\enar\right|
\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre_c/4.png)
et donc,
![\[D(a)=-(2+a)(1-a)(a-1)=(2+a)(1-a)^2\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre_c/5.png)
Ainsi, la famille est une base si et seulement si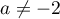 et
et 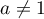 .
.
Correction
Le déterminant des 3 vecteurs est:![\[D(a)=\left|\begin{array}{ccc}a&1&1\\1&a&1\\1&1&a\enar\right|\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre_c/1.png)
La famille est libre, donc une base, si et seulement si
En ajjoutant les 3 colonnes dans la 1ère, on obtient,
![\[D(a)=\left|\begin{array}{ccc}2+a&1&1\\2+a&a&1\\2+a&1&a\enar\right|
=(2+a)\left|\begin{array}{ccc}1&1&1\\1&a&1\\1&1&a\enar\right|\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre_c/3.png)
puis en soustrayant la 2ème colonne à la 1ère,
![\[D(a)=(2+a)\left|\begin{array}{ccc}0&1&1\\1-a&a&1\\0&1&a\enar\right|
=-(2+a)(1-a)\left|\begin{array}{cc}1&1\\1&a\enar\right|
\]](/Generateur-Devoirs/Colles/determinants/exFamille-libre_c/4.png)
et donc,
Ainsi, la famille est une base si et seulement si
Tags:Espace vectorielDéterminants
Autres sujets au hasard:

Voir aussi: