Intégrales trigonométriques et famille de fonctions trigonométriques libre
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
- Espace vectorielEspaces vectoriels
Énoncé du sujet
- Pour
 et
et  des entiers naturels donnés, calculer
les intégrales
des entiers naturels donnés, calculer
les intégrales
 ,
,
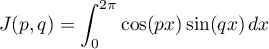 , et
, et
 .
.
- Montrer que la famille de fonctions
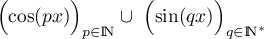 est libre.
est libre.
Correction
Correction
- On pose, pour
 ,
,
 ,
tel que,
si
,
tel que,
si  ,
,
![$E(p,q)=\dfrac1{p+q}\Bigr[e^{(p+q)x}\Bigr]_0^{2\pi}=0$](/Generateur-Devoirs/Colles/Integrale/exFamilleTrigo_c/4.png) ,
tandis que
,
tandis que  .
.
On a aussi en développant les produits d'exponentielles complexes, ,
et aussi, en utilisant la parité des fonctions cosinus et sinus:
,
et aussi, en utilisant la parité des fonctions cosinus et sinus:
 .
.
On a donc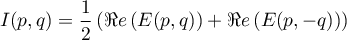 ,
,
et ainsi, si ,
,  ,
,  , et sinon
, et sinon  .
.
De même,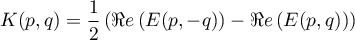 ,
et ainsi,
si
,
et ainsi,
si 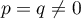 ,
,  , sinon,
, sinon,  .
.
Enfin, ,
et donc, comme
,
et donc, comme 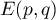 est réel,
pour tous
est réel,
pour tous  et
et  ,
,  .
.
- On considère une sous famille finie quelconque,
c'est-à-dire deux ensembles finis d'entiers:
 et
et  et une combinaison linéaire nulle:
et une combinaison linéaire nulle:
![\[\sum_{p\in A}\lambda_p \cos(px)+\sum_{q\in B}\mu_q \sin(qx)=0\]](/Generateur-Devoirs/Colles/Integrale/exFamilleTrigo_c/24.png)
Soit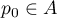 , alors, en multipliant par
, alors, en multipliant par
 puis en intégrant entre
puis en intégrant entre  et
et  , on obtient:
, on obtient:
![\[\begin{array}{ll}&\sum_{p\in A}\lambda_p I\left( p_0,p\rp+\sum_{q\in B}\mu_q J\left( p_o,q\rp=0\\[.6em]
\iff&\pi\lambda_{p_0}=0\enar\]](/Generateur-Devoirs/Colles/Integrale/exFamilleTrigo_c/29.png)
ainsi, et on obtient ainsi que tous les coefficients
et on obtient ainsi que tous les coefficients  sont
nécessairement nuls.
En multipliant de même par
sont
nécessairement nuls.
En multipliant de même par  pour chaque
pour chaque  et en intégrant, on obtient que
chaque coefficient
et en intégrant, on obtient que
chaque coefficient  est aussi nul.
est aussi nul.
Finalement, on a montré que toute famille extraite est libre, et donc que la famille est libre.
est libre.
Remarque: l'application est un produit scalaire
dans l'espace des fonctions continues sur
est un produit scalaire
dans l'espace des fonctions continues sur ![$[0;2\pi]$](/Generateur-Devoirs/Colles/Integrale/exFamilleTrigo_c/37.png) (à savoir (re)démontrer).
(à savoir (re)démontrer).
Les calculs intégraux du 1. montrent que la famille est orthogonale pour ce produit scalaire
et ne contient pas la fonction nulle: c'est donc une famille libre.
est orthogonale pour ce produit scalaire
et ne contient pas la fonction nulle: c'est donc une famille libre.
Tags:IntégraleEspace vectoriel
Autres sujets au hasard:

Voir aussi: