Limite exponentielle
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
Calculer la limite de la suite:
 ,
, 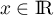
Correction
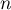 , on a
, on a
![\[u_n=\lp1+\dfrac{x}{n}\rp^n
=\exp\left( n\ln\left(1+\dfrac{x}{n}\rp\rp\]](/Generateur-Devoirs/Colles/Suites/limite-exp_c/2.png)
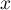 est un réel fixé, et
est un réel fixé, et 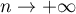 , d'où
, d'où
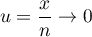 , et alors
, et alors
![\[\begin{array}{ll}
u_n&=\exp\left( n\left( u+o(u)\rp\rp\\[.5em]
&=\exp\left( nu +o(nu)\rp\\[.5em]
&=\exp\left( x+o(1)\rp\enar\]](/Generateur-Devoirs/Colles/Suites/limite-exp_c/6.png)
et la limite de lorsque
lorsque  est donc
est donc 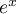 .
.
Correction
Pour tout entier![\[\begin{array}{ll}
u_n&=\exp\left( n\left( u+o(u)\rp\rp\\[.5em]
&=\exp\left( nu +o(nu)\rp\\[.5em]
&=\exp\left( x+o(1)\rp\enar\]](/Generateur-Devoirs/Colles/Suites/limite-exp_c/6.png)
et la limite de
Tags:SuitesLimiteDL
Autres sujets au hasard:

Voir aussi: