Convergence de la suite de racines d'un polynôme
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
- Montrer que l'équation
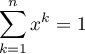 admet une unique solution
admet une unique solution 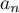 dans
dans ![$[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20/3.png) .
.
- Démontrer que
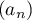 est décroissante et minorée par
est décroissante et minorée par  .
.
- Démontrer que
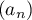 converge vers
converge vers  .
.
Correction
Correction
- Pour
 , l'équation s'écrit
, l'équation s'écrit  et
et 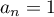 …
…
Soit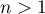 , on considère la fonction
, on considère la fonction 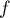 définie sur
définie sur ![$[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/6.png) par
par
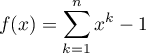 .
.
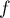 est un polynôme, donc continue et dérivable avec
est un polynôme, donc continue et dérivable avec
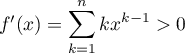 pour
pour ![$x\in]0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/10.png) et
et 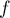 est donc strictement croissante sur
est donc strictement croissante sur ![$[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/12.png) .
.
De plus, aux bornes on a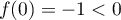 et
et 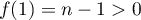 dès que
dès que 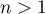 .
.
D'après le théorème des valeurs intermédiaires (ou de la bijection car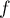 est ainsi une bijection entre
est ainsi une bijection entre ![$[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/17.png) et
et ![$[-1;n-1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/18.png) ),
il existe une unique valeur
),
il existe une unique valeur ![$a_n\in[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/19.png) telle que
telle que 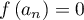 .
.
- On a donc
![$a_n\in[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/21.png) et
et 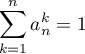 .
Pour étudier le sens de variation d'une suite, on s'intéresse assez naturellement à la différence de deux termes consécutifs
.
Pour étudier le sens de variation d'une suite, on s'intéresse assez naturellement à la différence de deux termes consécutifs
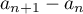 qu'on fait apparaître en faisant la différence
qu'on fait apparaître en faisant la différence
![\[\sum_{k=1}^{n+1}a_{n+1}^k-\sum_{k=1}^na_n^k=0\]](/Generateur-Devoirs/Colles/Suites/ex20_c/24.png)
soit
![\[a_{n+1}^{n+1}+\sum_{k=1}^n\left( a_{n+1}^k-a_n^k\rp=0\]](/Generateur-Devoirs/Colles/Suites/ex20_c/25.png)
ou encore, comme![$a_{n+1}\in[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/26.png) ,
,
![\[\sum_{k=1}^n\left( a_{n+1}^k-a_n^k\rp=-a_{n+1}^{n+1}<0\]](/Generateur-Devoirs/Colles/Suites/ex20_c/27.png)
Maintenant, comme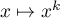 est strictement croissante sur
est strictement croissante sur ![$[0;1]$](/Generateur-Devoirs/Colles/Suites/ex20_c/29.png) pour tout entier
pour tout entier 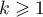 ,
on a, pour tout
,
on a, pour tout 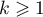 ,
,
![\[a_{n+1}-a_n<0\iff a_{n+1}<a_n\iff a_{n+1}^k<a_n^k\]](/Generateur-Devoirs/Colles/Suites/ex20_c/32.png)
Ainsi, tous les termes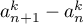 sont de même signe, et, leur somme étant négative d'après la relation précédente,
ils sont tous négatifs. En particulier
sont de même signe, et, leur somme étant négative d'après la relation précédente,
ils sont tous négatifs. En particulier 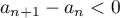 donc
donc 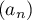 est décroissante.
est décroissante.
On a de plus,
![\[\begin{array}{ll}f\lp\dfrac12\rp&=\dsp\sum_{k=1}^n\lp\dfrac12\rp^k\\[1.2em]
&=\dfrac12\,\dfrac{1-\lp\dfrac12\rp^n}{1-\dfrac12}\\[2.1em]
&=1-\lp\dfrac12\rp^n<0\enar\]](/Generateur-Devoirs/Colles/Suites/ex20_c/36.png)
ce qui montre que, pour tout entier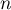 , on a,
, on a, 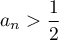 .
.
- La suite
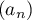 est décroissante et minorée; elle est donc convergente vers un réel
est décroissante et minorée; elle est donc convergente vers un réel 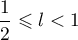 .
.
Miantenant, ce réel satisfait nécessairement, par passage à la limite,
![\[\begin{array}{ll}&\dsp\sum_{k=1}^\infty l^k=1\\[1em]
&\iff \dfrac{l}{1-l}=1\\[1em]
&\iff l=1-l\\[.9em]
&\iff l=\dfrac12\enar\]](/Generateur-Devoirs/Colles/Suites/ex20_c/41.png)
Tags:SuitesSommes
Autres sujets au hasard:

Voir aussi: