Calcul de limite avec le théorème des accroissements finis
Colle de mathématiques
Sujet de colle de maths:- LimiteLimites de suites et de fonctions
- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Utiliser le théorème des accroissements finis,
appliqué à la fonction 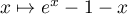 pour démontrer que:
pour démontrer que:
![\[\lim_{x\rightarrow 0} \frac{e^x-1-x}{x^2}=\frac{1}{2}\]](/Generateur-Devoirs/Colles/Calcul/exlimAF2/2.png)
Correction
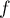 définie par
définie par 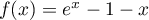 :
il existe
:
il existe ![$c\in]0;x[$](/Generateur-Devoirs/Colles/Calcul/exlimAF2_c/3.png) tel que
tel que
![\[f(x)-f(0)=(x-0)f'(c)=x\left( e^c-1\rp\]](/Generateur-Devoirs/Colles/Calcul/exlimAF2_c/4.png)
On applique une deuxième fois le théorème des accroissements finis, à la fonction définie par
définie par  ,
sur
,
sur ![$]0;c[$](/Generateur-Devoirs/Colles/Calcul/exlimAF2_c/7.png) : il existe
: il existe ![$d\in]0;c[$](/Generateur-Devoirs/Colles/Calcul/exlimAF2_c/8.png) tel que
tel que
![\[g(c)-g(0)=(c-0)g'(d) \iff e^c-1=ce^d\]](/Generateur-Devoirs/Colles/Calcul/exlimAF2_c/9.png)
En résumé, on a obtenu, avec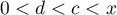 ,
,
![\[f(x)-f(0)=e^x-1-x=x\left( e^c-1\rp=xce^d<x^2e^x\]](/Generateur-Devoirs/Colles/Calcul/exlimAF2_c/11.png)
Correction
On applique le théorème des accroissements finis àOn applique une deuxième fois le théorème des accroissements finis, à la fonction
En résumé, on a obtenu, avec
Tags:LimiteRolle - AF
Autres sujets au hasard:

Voir aussi: