Intégrale trigonométrique
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
Calculer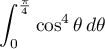 
Correction
:
![\[\cos^4\theta=\lp\dfrac{e^{i\theta}+e^{-i\theta}}{2}\rp^4
=\dfrac{1}{2^3}\left(
\dfrac{e^{4i\theta}+e^{-4i\theta}}{2}
+4\dfrac{e^{2i\theta}+e^{-2i\theta}}{2}
+\dfrac{6}{2}\right)
=\dfrac18\lp\cos(4\theta)+4\cos(2\theta)+3\rp\]](/Generateur-Devoirs/Colles/Complexes/ex11_c/2.png)
On calcule alors l'intégrale via une primitive:
![\[\int_0^{\frac\pi4} \cos^4\theta\,d\theta
\dfrac18\Bigl[ \dfrac14\sin(4\theta)+2\sin(2\theta)+3\theta\Bigr]_0^{\frac\pi4}
=\dfrac18\left( -\dfrac14+\dfrac{3\pi}{4}\right)
=\dfrac{1}{32}\lp3\pi-1\right)
\]](/Generateur-Devoirs/Colles/Complexes/ex11_c/3.png)
Correction
On linéarise:
On calcule alors l'intégrale via une primitive:
Tags:IntégraleComplexes
Autres sujets au hasard:
Voir aussi: