Équation différentielle - 1er ordre, coefficients non constants
Colle de mathématiques
Sujet de colle de maths:- Équation différentielleÉquation différentielle
Énoncé du sujet
Résoudre sur ![$]0;+\infty[$](/Generateur-Devoirs/Colles/EquaDiff/ex5.3/1.png) l'équation différentielle:
l'équation différentielle:
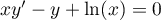 .
.
Correction
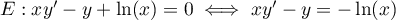 .
.
L'équation homogène associée est
![\[E_0: xy'-y=0
\iff \dfrac{y'}{y}=\dfrac1x\]](/Generateur-Devoirs/Colles/EquaDiff/ex5.3_c/2.png)
et donc, en intégrant,
![\[y=Cx\]](/Generateur-Devoirs/Colles/EquaDiff/ex5.3_c/3.png)
où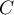 est une constante quelconque.
est une constante quelconque.
Pour Déterminer une solution particulière de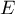 ,
on peut essayer de faire varier la constante:
,
on peut essayer de faire varier la constante:
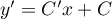 et alors
et alors
![\[xy'-y=-\ln(x)
\iff C'x=\ln(x)
\iff C'=\dfrac{\ln(x)}{x}\]](/Generateur-Devoirs/Colles/EquaDiff/ex5.3_c/7.png)
On peut alors directement intégrer, car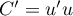 avec
avec 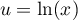 ,
et donc
,
et donc 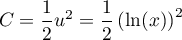 .
.
Les solutions de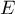 sont donc les fonctions qui s'écrivent sous la forme,
sont donc les fonctions qui s'écrivent sous la forme,
![\[y(x)=x\lp\ln(x)\rp^2+Cx\]](/Generateur-Devoirs/Colles/EquaDiff/ex5.3_c/12.png)
pour toute constante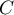 .
.
Correction
SoitL'équation homogène associée est
et donc, en intégrant,
où
Pour Déterminer une solution particulière de
On peut alors directement intégrer, car
Les solutions de
pour toute constante
Tag:Équation différentielle
Autres sujets au hasard:

Voir aussi: