Egalité de sous-espaces vectoriels et supplémentaire


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

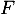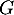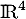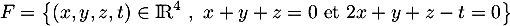
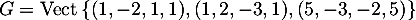Soit $F$ et $G$ les sous-espaces vectoriels de $\R^4$ suivants: $F=\left\{ (x,y,z,t)\in \R^4 \ , \ x+y+z=0 \text{ et } 2x+y+z-t=0 \right\}$ $G=\text{Vect}\left\{ (1,-2,1,1),(1,2,-3,1),(5,-3,-2,5)\right\}$.
  1. Montrer que 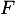$F$ est un espace vectoriel et donner sa dimension de $F$.
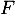  2. Montrer que 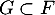$G\subset F$ et conclure que $G=F$.
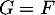  3. Déterminer un supplémentaire de $F$.



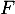Correction

Correction

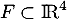  1. On a $F\subset\R^4$ et on peut montrer qu'il s'agit d'un sous-espace vectoriel, stable par combinaison linéaire.
    On peut aussi montrer que l'ensemble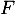 $F$ est généré par certains vecteurs. Pour cela, on écrit que
    \[\begin{array}{ll} (x,y,z,t)\in F&\iff \la\begin{array}{rcl} x+y+z&=&0\\ 2x+y+z-t&=&0\\ \enar\right. \\[1.2em] &\iff\la\begin{array}{rcl} x+y+z&=&0\\ x+(x+y+z)-t&=&0\\ \enar\right. \\[1.2em] &\iff \left\{\begin{array}{rcl} x+y+z&=&0\\ x-t&=&0\\ \end{array}\right. \\[1.2em] &\iff \left\{\begin{array}{rcl} x&=&x\\ y&=&-x-z\\ z&=&z\\ t&=&x\\ \end{array}\right. \enar\]

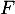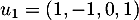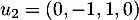    On en déduit que $F$ est généré par les vecteurs $u_1=(1,-1,0,1)$ et $u_2=(0,-1,1,0)$, c'est-à-dire 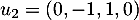$F=\text{Vect}\left\{}\newcommand{\ra}{\right\} u_1,u_2\ra$, ce qui montre au passage que 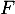$F$ est bien un sous-espace vectoriel.
    Ces deux vecteurs sont de plus libres (non colinéaires), et forment donc une base de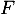 $F$ qui est alors de dimension 2.
  2. Il suffit de montrer que les quatre vecteurs engendrant 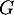$G$ sont aussi des vecteurs de 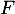$F$, ce qui est direct en remplaçant les coordonnées de chaque vecteur dans les deux équations définissant $F$.
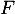    On en déduit en particulier que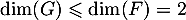 $\dim(G)\leqslant\dim(F)=2$.
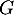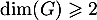    Or, en prenant par exemple les deux premiers vecteurs de $G$ qui sont libres entre eux (à nouveau car non colinéaires), on a que $\dim(G)\geqslant2$.
    Finalement, on a nécessairement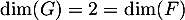 $\dim(G)=2=\dim(F)$ et comme on a montré que 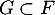$G\subset F$, ceci finit de montrer que $G=F$.
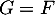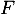  3. $F$ est de dimension 2, et 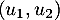$(u_1,u_2)$ est une base de $F$.
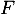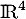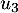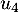    D'après le théorème de la base incomplète, on sait qu'on peut compléter cette famille en une base de $\R^4$ avec deux vecteurs $u_3$ et $u_4$ choisis dans la base canonique de 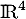$\R^4$. Ces deux vecteurs utilisés pour compléter engendre alors un supplémentaire de $F$.
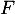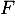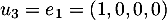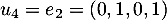    Il suffit donc de choisir deux vecteurs de la base canonique qui ne sont pas dans $F$, par exemple $u_3=e_1=(1,0,0,0)$ et $u_4=e_2=(0,1,0,1)$.
    Ainsi, avec ces deux vecteurs,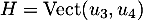 $H=\text{Vect}(u_3,u_4)$ est un supplémentaire de 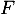$F$ dans $R^4$.


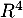Tag:Espace vectoriel

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0