Supplémentaire de l'ensemble des fonctions affines
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit 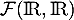 l'ensemble des fonctions de
l'ensemble des fonctions de 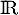 dans
dans 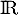 , et
, et 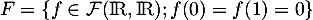 et
et 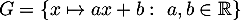 .
.
- Démontrer que
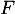 et
et 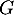 sont des sous-espaces vectoriels de
sont des sous-espaces vectoriels de 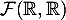 .
.
- Démontrer que
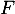 et
et 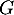 sont en somme directe.
sont en somme directe.
- Soit
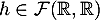 . Déterminer deux réels
. Déterminer deux réels 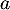 et
et 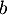 tels que la fonction
tels que la fonction 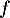 définie pour tout
définie pour tout 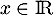 par
par 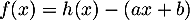 vérifie
vérifie 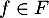 .
.
- En déduire que
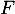 et
et 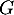 sont supplémentaires dans
sont supplémentaires dans 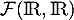 .
.
Correction
Correction
- On montre que ces sous-espaces sont stables par combinaison linéaire.
Soit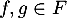 . Alors
. Alors 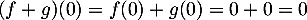 et
et 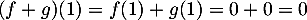 , ce qui montre que
, ce qui montre que 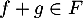 .
.
De même, pour tout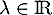 , on a
, on a 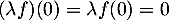 et
et 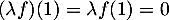 ce qui montre cette fois que
ce qui montre cette fois que 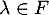 .
.
On en déduit donc que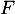 est stable par combinaison linéaire et donc
est stable par combinaison linéaire et donc 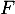 est un sous-espace vectoriel de
est un sous-espace vectoriel de 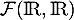 .
.
De la même façon, on prouve que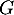 est un sous-espace vectoriel de
est un sous-espace vectoriel de 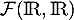 .
.
Si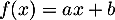 et
et 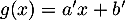 , alors
, alors 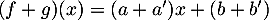 et donc
et donc 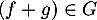 , et de même
, et de même
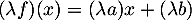 donc
donc 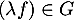 .
.
Ainsi,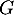 est aussi un sous-espace vectoriel de
est aussi un sous-espace vectoriel de 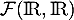 .
.
- Soit
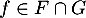 . Alors il existe
. Alors il existe 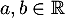 tel que, pour tout
tel que, pour tout 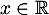 ,
, 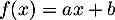 . Puisque
. Puisque 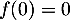 , on a forcément
, on a forcément 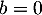 . Puis, puisque
. Puis, puisque 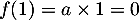 , on a aussi
, on a aussi
 . Ainsi,
. Ainsi, 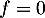 et on a bien
et on a bien 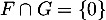 , c'est-à-dire que
, c'est-à-dire que 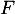 et
et 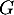 sont en somme directe.
sont en somme directe.
- On a
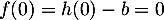 , et donc
, et donc 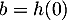 . On a
. On a 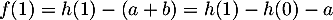 , et donc
, et donc 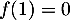 dès que
dès que 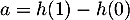 .
.
- Soit
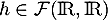 . En suivant la question précédente, on pose
. En suivant la question précédente, on pose 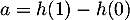 et
et 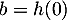 et la fonction
et la fonction 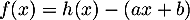 .
.
On a alors, d'après la question précédente,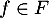 .
De plus, on peut écrire pour tout
.
De plus, on peut écrire pour tout 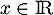 ,
,
![\[h(x)=f(x)+g(x)\]](/Generateur-Devoirs/Colles/ev/exssevaffine_c/45.png)
avec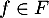 et
et 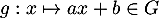 . On en déduit que
. On en déduit que 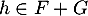 et donc que
et donc que 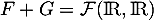 .
.
Comme on a aussi vu précédemment que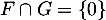 , on en déduit maintenant que
, on en déduit maintenant que 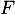 et
et 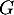 sont supplémentaires dans
sont supplémentaires dans 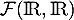 .
.
Tag:Espace vectoriel
Autres sujets au hasard:

Voir aussi: