Avec la trace de matrices
Colle de mathématiques
Sujet de colle de maths:- MatricesMatrices
- Espace vectorielEspaces vectoriels
Énoncé du sujet
Oral ESCP, BL - 2021
Dans cet exercice,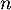 est un entier supérieur ou égal à 2 et
est un entier supérieur ou égal à 2 et  .
.
Pour toute matrice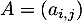 , on pose
, on pose 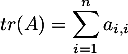 .
.
Dans cet exercice,
Pour toute matrice
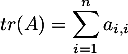 .
.
-
- Montrer que l'application
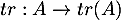 est linéaire.
est linéaire.
- Montrer que
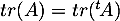 .
.
Dans la suite de l'exercice, on note:
![\[S_n(\R)=\left\{}\newcommand{\ra}{\right\} M\in\mathcal{M}_n(\R) / M=\, ^t\!M\ra\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11/7.png)
et
![\[A_n(\R)=\left\{}\newcommand{\ra}{\right\} M\in\mathcal{M}_n(\R) / M= -^t\!M\ra\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11/8.png)
- Montrer que l'application
- Montrer que
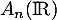 et
et 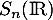 sont supplémentaires dans
sont supplémentaires dans 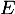 .
.
Pour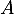 de
de  , on note
, on note 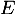 .
.
- Montrer que
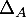 est un sous-espace vectoriel de
est un sous-espace vectoriel de 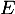 tel que
tel que  .
.
- Soit
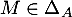 . Montrer que
. Montrer que 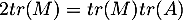 .
.
- Déterminer
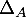 en discutant suivant les valeurs de
en discutant suivant les valeurs de 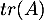 .
.
Correction
Correction
Oral ESCP, BL - 2021-
- En détaillant par exemple des matrices générales, on a directement que
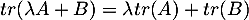 .
.
- Par transposition, les éléments diagonaux d'une matrice sont invariants, et donc, en particulier, une matrice et sa transposée ont la même trace.
- En détaillant par exemple des matrices générales, on a directement que
- Soit
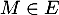 .
.
On pose
![\[A=\dfrac12\left( A - ^t\!A\rp\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/3.png)
et
![\[B=\dfrac12\left( A + ^t\!A\rp\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/4.png)
telles que et
et  , c'est-à-dire que
, c'est-à-dire que
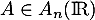 et
et 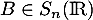 , et que
, et que
![\[M=A+B\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/9.png)
On a donc montré la somme
![\[E=A_n(\R)+B_n(\R)\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/10.png)
Il reste à montrer que cette somme est directe. Si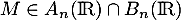 , alors
, alors
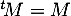 et
et  , d'où
, d'où 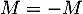 et donc
et donc 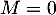 .
.
Ainsi l'intersection de ces deux sous-espaces est réduit à la matrice nulle, et on en déduit que la somme est directe:
![\[E=A_n(\R)\oplus B_n(\R)\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/16.png)
- Par linéarité de la trace et de la tansposition,
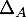 est un sous-espace vectoriel de
est un sous-espace vectoriel de 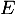 :
:
- la matrice nulle appartient à

- Pour
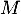 ,
,  de
de 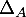 ,
donc
,
donc 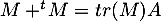 et
et 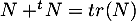 A,
et un réel
A,
et un réel 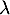 , on a
, on a
![\[\begin{array}{lcl}&&(\lambda M+N)+^t\!(\lambda M+N)\\
&=&\lambda (M+^t\!M)+N+^t\!N\\
&=&\lambda tr(M)A+tr(N)A\\
&=&\left( \lambda tr(M)+tr(N)\right) A\\
&=&tr(\lambda M+N)A\enar\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/26.png)
d'où
De plus, si , alors
, alors 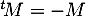 donc
donc  , et par ailleurs ces éléments diagonaux sont nuls, d'où
, et par ailleurs ces éléments diagonaux sont nuls, d'où 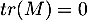 . Ainsi,
. Ainsi, 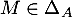 .
.
On en conclut que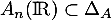 .
.
- la matrice nulle appartient à
- Si
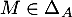 , alors
, alors
![\[M+^t\!M=tr(M)A\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/35.png)
et donc, en appliquant la trace, qui est linéaire,
![\[\begin{array}{ll}&tr\left( M+^t\!M\rp=tr\left( tr(M)A\rp\\
\iff&tr(M)+tr(M)=tr(M)tr(A)\\
\iff&2tr(M)=tr(M)tr(A)
\enar\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/36.png)
- La relation précédente se réécrit
![\[(2-tr(A))tr(M)=0\]](/Generateur-Devoirs/Colles/matrices/ESCP-BL-2021-4.11_c/37.png)
et donc est une valeur particulière.
est une valeur particulière.
- si
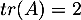 la relation de la question précédente est triviale, et il faut encore distinguer:
si
la relation de la question précédente est triviale, et il faut encore distinguer:
si 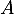 n'est pas symétrique, il n'y a pas de solution et
n'est pas symétrique, il n'y a pas de solution et 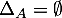 , tandis que si
, tandis que si 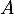 est symétrique, alors
est symétrique, alors 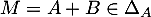 pour tout
pour tout 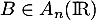 .
.
- si
 , alors on doit avoir
, alors on doit avoir  et donc, par définition de
et donc, par définition de 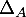 , on a
, on a 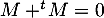 , d'où
, d'où 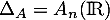
- si
Tags:MatricesEspace vectoriel
Autres sujets au hasard:
