Diagonalisabilité d'une application linéaire entre polynomes


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

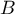  1. Soit $A$ et $B$ deux réels et $f:]0;1[\to\R$ une fonction de classe $\mathcal{C}^1$ qui vérifie, pour tout $x\in]0;1[$,
    \[f'(x)=\lp\dfrac{A}x+\dfrac{B}{x-1}\right) f(x)\]


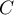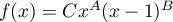    Montrer qu'il existe une constante $C$ telle que, pour tout $x\in]0;1[$, $f(x)=Cx^A(x-1)^B$.
    [.6em] Indication: on pourra considérer la fonction définie par $g(x)=\dfrac{f(x)}{x^A(x-1)^B}$
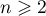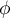  2. Soit un entier $n\geqslant2$ et $\phi$ l'application $\phi:\la\begin{array}{cll}\R_n[X]&\to&\R_n[X]\\[.4em] P&\mapsto&X(X-1)P'-n(X+1)P\enar\right.$
    1. Montrer que 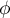$\phi$ est un endomorphisme de $\R_n[X]$.
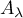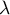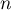    2. Soit $\lambda\in\R$. Montrer qu'il existe deux réels $A_\lambda$ et $B_\lambda$ (qui dépendent de $\lambda$ et $n$) tels que
      \[\forall x\in]0;1[\,, \ \dfrac{n(x+1)+\lambda}{x(x-1)}=\dfrac{A_\lambda}{x}+\dfrac{B_\lambda}{x-1}\]

    3. Montrer que $\phi$ est diagonalisable.



Correction

Correction

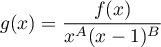  1. Soit $g(x)=\dfrac{f(x)}{x^A(x-1)^B}$. En prenant le logarithme, on a
    \[\ln(g(x))=\ln(f(x))-A\ln(x)-B\ln(x-1)\]

    et alors, en dérivant,
    \[\dfrac{g'(x)}{g(x)}=\dfrac{f'(x)}{f(x)}-\dfrac{A}x-\dfrac{B}{x-1}\]

    et alors,
    \[f'(x)=f(x)\lp\dfrac{A}x+\dfrac{B}{x-1}\rp+\dfrac{g'(x)}{g(x)}\times f(x)\]

    On obtient donc que
    \[f'(x)=f(x)\lp\dfrac{A}x+\dfrac{B}{x-1}\right) \iff \dfrac{g'(x)}{g(x)}\times f(x)=0\]

    et donc, soit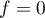 $f=0$, soit 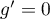$g'=0$ donc $g=c$.
    En revenant à la définition de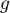 $g$, on a donc 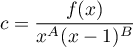$c=\dfrac{f(x)}{x^A(x-1)^B}$, qui est le résultat souhaité sur $f$.
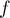    Remarque: on peut aussi directement dériver la fonction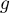 $g$.
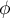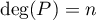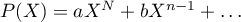    1. Par linéarité de la dérivée, l'application $\phi$ est aussi linéaire. De plus, si $P\in\R_n[X]$, alors $\text{deg}(P)=n$ avec $P(X)=aX^N+bX^{n-1}+\dots$ et alors
      \[\phi(P)=X(X-1)\left( anX^{n-1}+b(n-1)X^{n-2}+\dots\right) -n(X+1)\left( aX^n+bX^{n-1}+\dots\right)\]

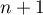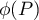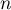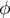      les termes de degré $n+1$ s'annulent, et le polynôme $\phi(P)$ est donc de degré $n$, soit $\phi(P)\in\R_n[X]$, ce qui finit de montrer que $\phi$ est bien un endomorphisme de $\R_n[X]$
    2. Il suffit de mettre sur le même dénominateur:
      \[\dfrac{A_\lambda}x+\dfrac{B_\lambda}{x-1} =\dfrac{\left( A_\lambda+B_\lambda\right) x-A_\lambda}{x(x-1)} =\dfrac{nx+n+\lambda}{x(x-1)}\]

      et on doit donc avoir
      \[\la\begin{array}{ll}A_\lambda+B_\lambda&=n\\-A_\lambda&=n+\lambda\enar\right. \iff\la\begin{array}{ll}A_\lambda&=-n-\lambda\\B_\lambda&=2n+\lambda\enar\right. \]

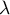    3. Soit $\lambda$ une valeur propre de 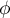$\phi$, alors il existe un polynôme $P\in\R_n[X]$ non nul tel que
      \[\begin{array}{ll} \phi(P)=\lambda P &\iff X(X-1)P'-n(X+1)P=\lambda P\\[.5em] &\iff P'=\dfrac{n(X+1)+\lambda}{X(X-1)}P\enar\]

      soit, d'après la question précédent,
      \[P'=\lp\dfrac{A_\lambda}X+\dfrac{B_\lambda}{X-1}\right) P\]

      et alors, d'après la première question, il existe une constante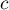 $c$ tel que
      \[P(X)=cX^{A_\lambda}(X-1)^{B_\lambda}\]

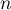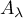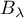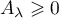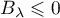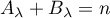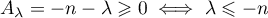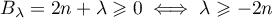      Maintenant, cette expression est un polynôme de degré au plus $n$ lorsque $A_\lambda$ et $B_\lambda$ sont des entiers tels que $A_\lambda\geqslant0$, $B_\lambda\leqslant0$ et $A_\lambda+B_\lambda=n$. D'après la question précédente, la troisième relation est assurée, tandis que les deux autres s'écrivent: $A_\lambda=-n-\lambda\geqslant0\iff \lambda\leqslant-n$ et $B_\lambda=2n+\lambda\geqslant0\iff\lambda\geqslant-2n$. 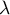En résumé, $\lambda$ doit être un entier tel que
      \[-2n\leqslant\lambda\leqslant-n\]

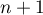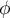      Il y a $n+1$ tels entiers, qui est aussi la dimension de $\R_n[X]$. Ainsi, $\phi$ n' que des valeurs propres simples, et est diagonalisable.


Tags:DiagonalisationPolynôme

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0