Racine cubique d'une matrice
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
- MatricesMatrices
Énoncé du sujet
Soit 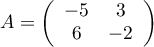 .
Montrer que
.
Montrer que  est diagonalisable et calculer ses valeurs propres.
est diagonalisable et calculer ses valeurs propres.
En déduire qu'il existe une matrice telle que
telle que
 .
.
En déduire qu'il existe une matrice
Correction
Avec le polynôme caractéristique:
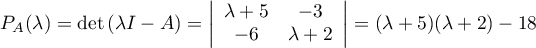
1 et racine évidente, et on on a alors la factorisation
![\[P_A(\lambda)=(\lambda-1)(\lambda+8)\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/2.png)
qui montre que le polynôme cacactéristique admet deux valeurs propres distinctes et donc, en particulier, que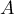 est diagonalisable.
est diagonalisable.
Il existe donc une matrice de passage inversible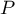 telle que
telle que 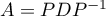 , avec
, avec
![\[D=\lp\begin{array}{cc}1&0\\0&-8\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/6.png)
On trouve facilement une racine cubique de cette dernière:
![\[B=\lp\begin{array}{cc}1&0\\0&-2\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/7.png)
est bien telle que .
.
Maintenant, la matrice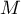 définie par
définie par
![\[M=PBP^{-1}\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/10.png)
vérifie
![\[M^3=PB^3P^{-1}=PDP^{-1}=A\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/11.png)
Avec un calcul de rang: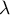 est une valeur propre lorsque
est une valeur propre lorsque 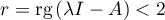 , soit
, soit
![\[r=\lp\lambda I-A\right)
=\lp\begin{array}{cc}\lambda+5&-3\\-6&\lambda+2\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/14.png)
soit, avec l'opération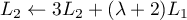 ,
,
![\[r=\lp\begin{array}{cc}\lambda+5&-3\\-18+(\lambda+2)(\lambda+5)&0\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/16.png)
On cherche donc les racines du trinôme du second degré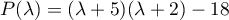 qui sont 1 (évidente) et -8.
qui sont 1 (évidente) et -8.
Ainsi, il y a deux valeurs propres distinctes et donc, en particulier,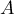 est diagonalisable.
est diagonalisable.
Il existe donc une matrice de passage inversible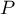 telle que
telle que 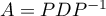 , avec
, avec
![\[D=\lp\begin{array}{cc}1&0\\0&-8\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/21.png)
On trouve facilement une racine cubique de cette dernière:
![\[B=\lp\begin{array}{cc}1&0\\0&-2\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/22.png)
est telle que .
.
On a alors que la matrice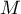 définie par
définie par
![\[M=PBP^{-1}\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/25.png)
vérifie
![\[M^3=PB^3P^{-1}=PDP^{-1}=A\]](/Generateur-Devoirs/Colles/Diagonalisation/Racine-cubique-matrice_c/26.png)
Correction
On commence par rechercher les valeurs propres pour diagonaliser cette matrice.Avec le polynôme caractéristique:
1 et racine évidente, et on on a alors la factorisation
qui montre que le polynôme cacactéristique admet deux valeurs propres distinctes et donc, en particulier, que
Il existe donc une matrice de passage inversible
On trouve facilement une racine cubique de cette dernière:
est bien telle que
Maintenant, la matrice
vérifie
Avec un calcul de rang:
soit, avec l'opération
On cherche donc les racines du trinôme du second degré
Ainsi, il y a deux valeurs propres distinctes et donc, en particulier,
Il existe donc une matrice de passage inversible
On trouve facilement une racine cubique de cette dernière:
est telle que
On a alors que la matrice
vérifie
Tags:DiagonalisationMatrices
Autres sujets au hasard:

Voir aussi: