Application linéaire ? Noyau et image ?
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
- PolynômePolynômes
Énoncé du sujet
Montrer que
![$f:\la\begin{array}{ll}\R[X]\to \R[X] \\[.4em] P\mapsto P-XP'\enar\right.$](/Generateur-Devoirs/Colles/Applin/exAL7/1.png) est une application linéaire.
est une application linéaire.
Déterminer son noyau et son image.
![$f:\la\begin{array}{ll}\R[X]\to \R[X] \\[.4em] P\mapsto P-XP'\enar\right.$](/Generateur-Devoirs/Colles/Applin/exAL7/1.png) est une application linéaire.
est une application linéaire.
Déterminer son noyau et son image.
Correction
![$P,Q\in\R[X]$](/Generateur-Devoirs/Colles/Applin/exAL7_c/1.png) et
et 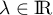 .
Alors
.
Alors
![\[\begin{array}{lcl}
f(\lambda P+Q)&=&(\lambda P+Q)-X(\lambda P+Q)'\\
&=&\lambda P+Q-X(\lambda P'+Q')\\
&=&\lambda (P-XP')+Q-XQ'=\lambda f(P)+ f(Q).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL7_c/3.png)
Ainsi, est bien une application linéaire.
est bien une application linéaire.
On s'intéresse au noyau de , donc
, donc
 .
.
Soit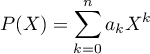 .
Alors on a:
.
Alors on a:
![\[f(P)=P-XP'=\sum_{k=1}^n (a_k-k a_{k})X^k +a_0\]](/Generateur-Devoirs/Colles/Applin/exAL7_c/8.png)
On en déduit que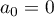 et que, pour tout entier
et que, pour tout entier 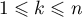 ,
,  .
.
Ainsi,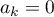 pour
pour  , et
, et 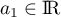 étant quelconque.
étant quelconque.
On en déduit que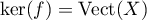 .
.
D'autre part, soit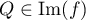 , avec
, avec  .
Alors, il existe
.
Alors, il existe 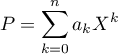 tel que
tel que  soit, d'après le calcul précédent,
soit, d'après le calcul précédent,
![\[b_k=a_k(1-k).\]](/Generateur-Devoirs/Colles/Applin/exAL7_c/20.png)
On en déduit et donc
et donc 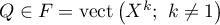 .
.
Réciproquement, soit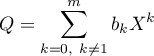 un élément de
un élément de
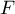 , c'est-à-dire un polynôme sans terme en
, c'est-à-dire un polynôme sans terme en 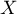 . Alors, si on pose
. Alors, si on pose 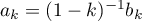 ,
, 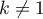 , et
, et 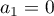 ,
le calcul précédent montre que
,
le calcul précédent montre que 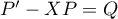 et donc
et donc  .
.
Ainsi,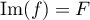 .
.
L'image et le noyau de sont de plus ici supplémentaires.
sont de plus ici supplémentaires.
Correction
Soit![\[\begin{array}{lcl}
f(\lambda P+Q)&=&(\lambda P+Q)-X(\lambda P+Q)'\\
&=&\lambda P+Q-X(\lambda P'+Q')\\
&=&\lambda (P-XP')+Q-XQ'=\lambda f(P)+ f(Q).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL7_c/3.png)
Ainsi,
On s'intéresse au noyau de
Soit
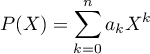 .
Alors on a:
.
Alors on a:
![\[f(P)=P-XP'=\sum_{k=1}^n (a_k-k a_{k})X^k +a_0\]](/Generateur-Devoirs/Colles/Applin/exAL7_c/8.png)
On en déduit que
Ainsi,
On en déduit que
D'autre part, soit
 .
Alors, il existe
.
Alors, il existe 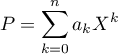 tel que
tel que On en déduit
Réciproquement, soit
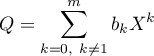 un élément de
un élément de
Ainsi,
L'image et le noyau de
Tags:Applications linéairesPolynôme
Autres sujets au hasard:

Voir aussi: