Décomposition de Fourier d'un signal périodique parabolique
Colle de mathématiques
Sujet de colle de maths:- Série de FourierSérie de Fourier
Énoncé du sujet
Soit 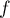 la fonction 2
la fonction 2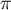 -périodique définie par
-périodique définie par
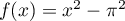 sur
sur 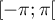 .
.
- Donner la série de Fourier de
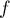 .
.
- Étudier sa convergence
- Calculer
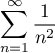
Correction
 la fonction 2
la fonction 2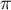 -périodique définie par
-périodique définie par
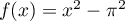 sur
sur 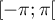 .
.
Correction
Soit- La fonction est 2
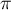 -périodique donc de pulsation
-périodique donc de pulsation 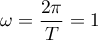 .
De plus,
.
De plus, 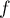 est paire, donc
est paire, donc 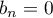 , et
, et
- sa valeur moyenne est
![\[\begin{array}{ll}a_0&=\dfrac{2}{T}\dsp\int_0^\pi f(x)\,dx \\[.8em]
&=\dfrac1\pi\dsp\int_0^\pi\left( x^2-\pi^2\rp\,dx\\[.8em]
&=\dfrac1\pi\Bigl[\,\dfrac{x^3}3-\pi^2 x\,\Bigr]_0^\pi\\[.8em]
&=\dfrac1\pi\lp\dfrac{\pi^3}3-\pi^3\rp=-\dfrac23\pi^2\enar\]](/Generateur-Devoirs/Colles/fourier/ex4_c/9.png)
- Pour tout entier
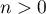 , en intégrant par parties,
, en intégrant par parties,
![\[\begin{array}{ll}a_n&=\dfrac4{2\pi}\dsp\int_0^\pi \left( x^2-\pi^2\rp\cos(nx)\,dx\\[.8em]
&=\dfrac2\pi\underbrace{\Bigl[\left( x^2-\pi^2\rp\dfrac{\sin(nx)}n\Bigr]_0^\pi}_{=0}
-\dfrac2\pi\dsp\int_0^\pi 2x\dfrac{\sin(nx)}n\,dx\\[.8em]
&=-\dfrac4{n\pi}\dsp\int_0^\pi x\sin(nx)\,dx
\enar\]](/Generateur-Devoirs/Colles/fourier/ex4_c/11.png)
puis, en intégrant une deuxième fois par parties,
![\[\begin{array}{ll}a_n&=\dsp-\dfrac4{n\pi}\Bigl[x\dfrac{-\cos(nx)}{n}\Bigr]_0^\pi
+\dfrac4{n\pi}\int_0^\pi\dfrac{-\cos(nx)}{n}\,dx\\[.8em]
&=\dfrac{4\pi\cos(n\pi)}{n^2\pi}
-\dfrac4{n^2\pi}\underbrace{\Bigl[\dfrac{\sin(nx)}n\Bigr]_0^\pi}_{=0}\\[.8em]
&=\dfrac{4(-1)^n}{n^2}\enar\]](/Generateur-Devoirs/Colles/fourier/ex4_c/12.png)
en utilisant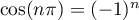 et
et 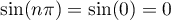 .
.
La fonction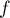 étant continue sur
étant continue sur 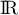 , on en déduit que pour tout réel
, on en déduit que pour tout réel 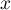 ,
,
![\[f(x)=-\dfrac23\pi^2+4\sum_{n\geqslant1}\dfrac{(-1)^n\cos(nx)}{n^2}\]](/Generateur-Devoirs/Colles/fourier/ex4_c/18.png)
- sa valeur moyenne est
- On a
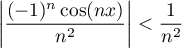 , ce qui montre que la série converge absolument en tout point.
, ce qui montre que la série converge absolument en tout point.
- En
 , on a alors, comme
, on a alors, comme 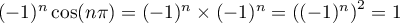 ,
,
![\[f(\pi)=0=-\dfrac23\pi^2+4\sum_{n\geqslant1}\dfrac1{n^2}\]](/Generateur-Devoirs/Colles/fourier/ex4_c/22.png)
et donc,
![\[\sum_{n=1}^{+\infty}\dfrac1{n^2}=\dfrac14\tm\dfrac23\pi^2=\dfrac{\pi^2}{6}\]](/Generateur-Devoirs/Colles/fourier/ex4_c/23.png)
Tag:Série de Fourier
Autres sujets au hasard:

Voir aussi: