Série de Fourier
Trois exemples de signaux et recomposition harmonique
Coefficients de Fourier
- La fonction a une moyenne nulle, donc
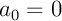 ,
,
- elle est impaire donc pour tout entier
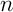 ,
, 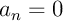
- elle est 2
 -périodique et impaire donc,
avec
-périodique et impaire donc,
avec  , pour tout entier
, pour tout entier  ,
,
et donc, les termes de rang pair sont nuls: 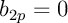 et ceux de rang impair valent
et ceux de rang impair valent
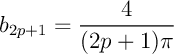 .
.
- On obtient alors, en tout poit où
 est continue,
donc pour tout
est continue,
donc pour tout 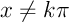 ,
,  ,
,
- La fonction est 2
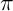 -périodique, continue sur
-périodique, continue sur  et affine par morceaux
avec,
pour tout
et affine par morceaux
avec,
pour tout ![$x\in[0;\pi]$](/Common/Fourier/CalculsIMG/16.png) ,
, 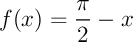 .
.
La fonction est paire donc, pour tout entier 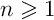 ,
, 
- sa valeur moyenne est aussi nulle:
- La pulsation est
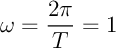 et alors,
pour tout entier
et alors,
pour tout entier 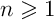 , on a
, on a
soit, en intégrant par parties,
et donc, puisque  ,
,
enfin, comme  ,
on obtient donc que les coefficients de rang pair sont nuls:
,
on obtient donc que les coefficients de rang pair sont nuls:
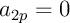 et ceux de rang impair valent
et ceux de rang impair valent
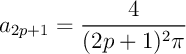
- Comme
 est continue sur
est continue sur  , on obtient pour tout
, on obtient pour tout  réel,
réel,
- La fonction est
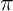 -périodique, donc de pulsation
-périodique, donc de pulsation
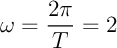 , et telle que
, et telle que
- sa valeur moyenne est
- Pour tout entier
 ,
,
et de même,
Finalement, en tout point 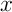 où
où 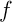 est continue
est continue
Voir aussi:
- Transformée de Fourier - Analyse harmonique

- Quelques autres calculs détaillés des coefficients de Fourier

- Cours sur les séries de Fourier

LongPage: h2: 1 - h3: 1
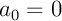 ,
,
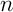 ,
, 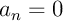
 -périodique et impaire donc,
avec
-périodique et impaire donc,
avec  , pour tout entier
, pour tout entier  ,
,
![\[\begin{array}{ll}
b_n&\dsp=\dfrac4T\int_0^\pi f(t)\sin\left( n\omega t\rp\,dt \\[1.2em]
&\dsp=\dfrac2\pi\int_0^\pi \sin\left( nt\rp\,dt \\[1.2em]
&\dsp=\dfrac2\pi\Bigl[\,-\dfrac{\cos(nt)}{n}\,\Bigr]_0^\pi\\[1.2em]
&\dsp=\dfrac2{n\pi}\Bigl(-\cos(n\pi)-1\Bigr)\\[1.2em]
&\dsp=\dfrac2{n\pi}\Bigl(1-(-1)^n\Bigr)
\enar\]](/Common/Fourier/CalculsIMG/7.png)
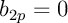 et ceux de rang impair valent
et ceux de rang impair valent
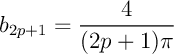 .
.
 est continue,
donc pour tout
est continue,
donc pour tout 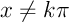 ,
,  ,
,
![\[f(x)=\dfrac4\pi\sum_{p\geqslant1}\dfrac{\sin\bigl((2p+1)x\bigr)}{2p+1}\]](/Common/Fourier/CalculsIMG/13.png)
![\[\begin{array}{ll}a_0&\dsp=\dfrac{1}{2\pi}\int_{-\pi}^\pi f(t)\,dt \\[1.2em]
&\dsp=\dfrac1\pi\int_0^\pi f(t)\,dt\\[1.2em]
&\dsp=\dfrac1\pi\int_0^\pi\lp\dfrac\pi2-t\rp\,dt\\[1.2em]
&\dsp=\dfrac1\pi\Bigl[\,\dfrac\pi2t-\dfrac{t^2}{2}\,\Bigr]_0^\pi\\[1em]
&=0
\enar\]](/Common/Fourier/CalculsIMG/20.png)
![\[\begin{array}{ll}
a_n&=\dsp\dfrac4T\int_0^\pi f(t)\cos(n\omega t)\,dt\\[1.2em]
&=\dsp\dfrac2\pi\int_0^\pi\lp\dfrac\pi2-t\rp\cos(nt)dt
\enar\]](/Common/Fourier/CalculsIMG/23.png)
![\[a_n=\dfrac2\pi\Bigr[\lp\dfrac\pi2-t\rp\dfrac{\sin(nt)}{n}\Bigr]_0^\pi
-\dfrac2\pi\int_0^\pi(-1)\dfrac{sin(nt)}{n}dt\]](/Common/Fourier/CalculsIMG/24.png)
![\[\begin{array}{ll}a_n&\dsp=\dfrac2{n\pi}\int_0^\pi\sin(nt)dt\\[1.2em]
&\dsp=\dfrac2{n\pi}\Bigl[-\dfrac{\cos(nt)}{n}\Bigr]_0^\pi
\enar\]](/Common/Fourier/CalculsIMG/26.png)
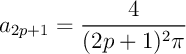
![\[f(x)=\dfrac4\pi\sum_{p\geqslant1}\dfrac{\cos\bigl((2p+1)x\bigr)}{(2p+1)^2}\]](/Common/Fourier/CalculsIMG/33.png)
(-2.14,0)
\psline[linecolor=blue,linewidth=2.2pt](-2.14,1)(-1.64,1)
\psline[linecolor=blue,linewidth=2.2pt](-1.64,0)(1,0)
\psline[linecolor=blue,linewidth=2.2pt](1,1)(1.5,1)
\psline[linecolor=blue,linewidth=2.2pt](1.5,0)(4.14,0)
\psline[linecolor=blue,linewidth=2.2pt](4.14,1)(4.64,1)
\psline[linecolor=blue,linewidth=2.2pt](4.64,0)(5,0)
\psline[linestyle=dashed,linewidth=.2pt,linecolor=blue](-1.64,0)(-1.64,1)
\psline[linestyle=dashed,linewidth=.2pt,linecolor=blue](-2.14,0)(-2.14,1)
\psline[linestyle=dashed,linewidth=.2pt,linecolor=blue](1,0)(1,1)
\psline[linestyle=dashed,linewidth=.2pt,linecolor=blue](1.5,0)(1.5,1)
\psline[linestyle=dashed,linewidth=.2pt,linecolor=blue](4.14,0)(4.14,1)
\psline[linestyle=dashed,linewidth=.2pt,linecolor=blue](4.64,0)(4.64,1)
\rput(1,-.25){$a$}\rput[l](1.4,-.2){$a\!+\!b$}
\psline[arrowsize=6pt]{<->}(.95,-.5)(1.55,-.5)
\rput(1.25,-.75){$b$}
\end{pspicture}\]](/Common/Fourier/CalculsIMG/36.png)
![\[a_0=\dfrac1\pi\int_0^\pi f(t)dt=\dfrac{b}\pi\]](/Common/Fourier/CalculsIMG/37.png)
![\[\begin{array}{ll}a_n&\dsp=\dfrac{2\pi}{T}\int_0^\pi f(t)\cos(n\omega t)dt\\[1.2em]
&=\dsp2\int_a^{a+b} \cos(2nt)dt\\[1.2em]
&\dsp=2\lb\dfrac{\sin(2nt)}{2n}\rb_a^{a+b}\\[1.2em]
&\dsp=\dfrac1n\Bigl(\sin\bigl(2n(a+b)\bigr)-\sin\bigl(2na\bigr)\Bigr)
\enar\]](/Common/Fourier/CalculsIMG/39.png)
![\[f(x)=\dfrac{b}{\pi}+\sum_{n\geqslant1}\Bigl( a_n\cos(2nx)+b_n\sin(2nx)\Bigr)\]](/Common/Fourier/CalculsIMG/43.png)