Calculer l'intégrale …


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

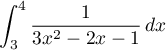
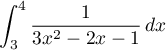
Calculer l'intégrale $\dsp\int_3^4 \dfrac{1}{3x^2-2x-1}\,dx$


Correction

Correction

On a, en décomposnt en éléments simples,
\[\dfrac{1}{3x^2-2x-1}=\dfrac{1}{(x-1)(3x+1)} =\dfrac{a}{x-1}+\dfrac{b}{3x+1}\]

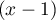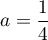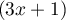et, en multipliant par $(x-1)$, puis en faisant $x=1$, on trouve $a=\dfrac14$, et de même, en multipliant par $(3x+1)$ et en faisant 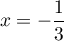$x=-\dfrac13$ on trouve 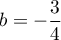$b=-\dfrac34$, soit, en résumé,
\[\dfrac{1}{3x^2-2x-1} =\dfrac14\tm\dfrac{1}{x-1}-\dfrac34\tm\dfrac{1}{3x+1}\]

et alors,
\[\begin{array}{ll} \dsp\int_3^4\dfrac{1}{3x^2-2x-1}dx &=\dsp\dfrac14\int_3^4\dfrac{1}{x-1}dx -\dfrac34\int_3^4\dfrac{1}{3x+1}dx\\[1.2em] &=\dfrac14\Bigl[\,\ln|x-1|\,\Bigr]_3^4 -\dfrac34\Bigl[\,\dfrac13\ln|3x+1|\,\Bigr]_3^4\\[1.2em] &=\dfrac14\ln\lp\dfrac32\rp-\dfrac14\ln\lp\dfrac{13}{10}\rp\\[1.2em] &=\dfrac14\ln\lp\dfrac{3\tm10}{2\tm13}\right) =\dfrac14\ln\lp\dfrac{15}{13}\right) \enar\]



Tag:Intégrale

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0