Intégrale impropre avec une fonction bornée et changement de variable

Colle de mathématiques

Sujet de colle de maths:

Soit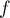

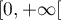une fonction continue bornée sur $[0,+\infty[$ .

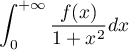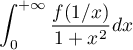Démontrer que les intégrales $\dsp\int_0^{+\infty}\frac{f(x)}{1+x^2}dx$ et $\dsp\int_0^{+\infty}\frac{f(1/x)}{1+x^2}dx$ sont convergentes.
Démontrer qu'elles sont égales.
Pour 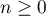$n\geq0$ , calculer $\dsp\int_0^{+\infty}\frac{dx}{(1+x^2)(1+x^n)}$ et $\dsp\int_0^{+\infty}\frac{x^n}{(1+x^2)(1+x^n)}dx.$

Correction

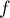est bornée, ce qui signifie qu'il existe 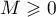$M\geqslant0$ tel que 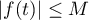$|f(t)|\leq M$ pour tout $t\in\R_+$ .
La fonction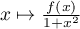 $x\mapsto \frac{f(x)}{1+x^2}$ est de plus continue sur $[0,+\infty[$ , et elle vérifie donc

$\left|\dfrac{f(x)}{1+x^2}\right|\leq\dfrac{M}{1+x^2}$

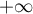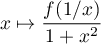qui est intégrable au voisinage de $+\infty$ . L'intégrale $\dsp\int_0^{+\infty}\frac{f(x)}{1+x^2}dx$ est ainsi convergente. De même, $x\mapsto \dfrac{f(1/x)}{1+x^2}$ est continue sur $]0,+\infty[$ (mais pas forcément en 0 cette fois).
Le problème en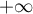 $+\infty$ se traite exactement comme précédemment, tandis qu'en 0, le quotient reste bornée même s'il n'est pas continu:

$\left|\frac{f(1/x)}{1+x^2}\right|\leq M$

et l'intégrale converge donc aussi en 0.
Avec le changement de variables , on trouve

$\int_0^{+\infty}\frac{f(x)}{1+x^2}dx =-\int_0^{+\infty}\frac{f(1/u)}{1+\frac{1}{u^2}}\frac{-1}{u^2}du =\int_0^{+\infty}\frac{f(1/x)}{1+x^2}dx$
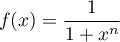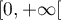On applique le résultat des questions précédentes avec $f(x)=\dfrac1{1+x^n}$ , qui est bien continue et bornée sur $[0,+\infty[$ . On trouve

$I=\int_0^{+\infty}\frac{dx}{(1+x^2)(1+x^n)} =\int_0^{+\infty}\frac{x^n}{(1+x^2)(1+x^n)}dx$

En effectuant la somme de ces deux intégrales, on trouve:

$2I=\int_0^{+\infty}\dfrac{1+x^n}{(1+x^2)(1+x^n)}dx =\int_0^{+\infty}\frac{dx}{1+x^2}=\frac\pi2$

On en déduit que ces deux intégrales sont à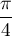 $\dfrac\pi4$ .

Tag:Intégrale

Autres sujets au hasard:

Voir aussi: