Suite implicite définie par une intégrale impropre
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
Soit 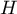 définie par:
définie par:
![\[H(x)=\int_x^{+\infty}\dfrac{e^{-t^2}}{2(1+t)}dt\]](/Generateur-Devoirs/Colles/Integrale/IISI/2.png)
et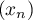 la suite définie par
la suite définie par 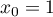 et
et
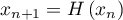 .
.
![\[H(x)=\int_x^{+\infty}\dfrac{e^{-t^2}}{2(1+t)}dt\]](/Generateur-Devoirs/Colles/Integrale/IISI/2.png)
et
- Déterminer les valeurs de
 pour lesquelles
pour lesquelles  est convergente.
est convergente.
- Étudier les variations de
 sur
sur ![$]0;+\infty[$](/Generateur-Devoirs/Colles/Integrale/IISI/9.png) . Préciser la limite en
. Préciser la limite en  .
.
- Prouver que
 pour tour entier
pour tour entier  .
.
- Montrer qu'il existe un unique
 tel que
tel que 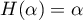 .
.
- Montrer que, pour tout entier
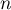 ,
,
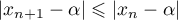 .
.
- En déduire que
 converge.
converge.
Correction
Correction
- La fonction
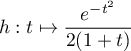 est continue sur
est continue sur
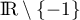 et, par croissances comparées en
et, par croissances comparées en 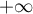 ,
,
![\[\lim_{t\to+\infty}t^2h(t)=0\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/4.png)
c'est-à-dire que
![\[h(t)=o\lp\dfrac1{t^2}\rp\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/5.png)
et donc par comparaison avec une intégrale de Riemann, l'intégrale est convergente en , et ainsi
, et ainsi
 est définie pour
est définie pour  .
.
En , on a
, on a 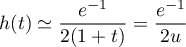 avec
avec  , et ainsi par comparaison avec une intégrale de Riemann (en 0 cette fois),
, et ainsi par comparaison avec une intégrale de Riemann (en 0 cette fois),  diverge en
diverge en  .
.
En résumé est définie sur
est définie sur ![$]-1;+\infty[$](/Generateur-Devoirs/Colles/Integrale/IISI_c/15.png) .
.
- On a
 et donc,
pour tout
et donc,
pour tout  ,
,
![\[H'(x)=-h(x)=-\dfrac{e^{-x^2}}{2(1+x)}\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/18.png)
Or,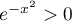 et
et 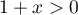 sur
sur ![$]0;+\infty[$](/Generateur-Devoirs/Colles/Integrale/IISI_c/21.png) et donc
et donc
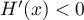 et
et  est décroissante.
est décroissante.
Comme l'intégrale est convergente, on a que
![\[\lim_{x\to+\infty}H(x)=\lim_{x\to+\infty}\int_x^{+\infty}h(t)dt=0\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/24.png)
Comme ce n'est pas nécessairement complètement évident, pour le montrer on peut par exemple décomposer l'intégrale en écrivant que, pour tous réels et
et 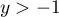
![\[H(x)-H(y)=\int_x^yh(t)dt\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/27.png)
soit aussi
![\[H(x)=H(y)-\int_x^yh(t)dt\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/28.png)
avec, puisque l'intégrale est convergente,
![\[\lim_{x\to+\infty}\int_x^yh(t)dt=\int_x^{+\infty}h(t)dt=H(y)\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/29.png)
d'où
![\[\lim_{x\to+\infty}H(x)=H()-H(y)=0\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/30.png)
- Pour tout réel
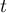 positif, on a
positif, on a
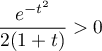 et donc, par positivité de l'intégrale,
et donc, par positivité de l'intégrale,
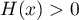 pour tout
pour tout 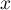 positif.
positif.
Ainsi, par récurrence,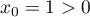 et lorsque
et lorsque  alors on a donc aussi
alors on a donc aussi
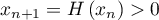 .
On a donc, pour tout entier
.
On a donc, pour tout entier 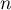 ,
, 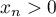 .
.
- On considère la fonction
 définie sur
définie sur  par
par 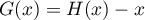 et on cherche
et on cherche 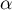 tel que
tel que 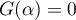 .
.
On a alors,
![\[G'(x)=-\dfrac{e^{-x^2}}{2(1+x)}-1<0\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/45.png)
comme on l'a vu précédemment, et ainsi est strictement décroissante.
est strictement décroissante.
On a de plus que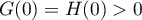 (positivité de l'intégrale, vu précédemment)
et, comme
(positivité de l'intégrale, vu précédemment)
et, comme  , on a
, on a
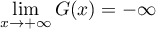 .
.
Comme est aussi continue (même dérivable), d'après le théorème de la bijection (car en effet
est aussi continue (même dérivable), d'après le théorème de la bijection (car en effet 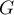 est une bijection de
est une bijection de 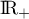 sur
sur 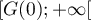 ), il existe un unique
), il existe un unique 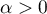 tel que
tel que 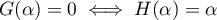 .
.
- Pour tout entier
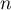 , on a
, on a
![\[\begin{array}{lcl}x_{n+1}-\alpha
&=&H(x_n)-H(\alpha)\\[.5em]
&=&\dsp\int_{x_n}^\alpha h(t)dt\enar\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/57.png)
et donc
![\[\left|x_{n+1}-\alpha\right|
\leqslant\left|x_n-\alpha\right|\max_{t\in[x_n;\alpha]}\left|h(t)\right|\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/58.png)
Or, pour tout entier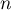 , on a vu que
, on a vu que 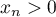 ,
et pour
,
et pour 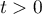 ,
,
![\[\left|h(t)\right|\leqslant\dfrac12<1\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/62.png)
On a bien obtenu ainsi que
![\[\left|x_{n+1}-\alpha\right|\leqslant\left|x_n-\alpha\right|\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/63.png)
- On a vu à la question précédente, que plus précisément on a
![\[\left|x_{n+1}-\alpha\right|\leqslant\dfrac12\left|x_n-\alpha\right|\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/64.png)
et donc, par une récurrence immédiate,
![\[\left|x_n-\alpha\right|\leqslant\dfrac1{2^n}\left|x_0-\alpha\right|\]](/Generateur-Devoirs/Colles/Integrale/IISI_c/65.png)
ce qui montre que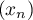 converge vers
converge vers 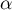 .
.
Tags:IntégraleSuites
Autres sujets au hasard:

Voir aussi: