Matrice d'une application linéaire dans des bases pas canoniques
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
- MatricesMatrices
- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit  l'application linéaire de
l'application linéaire de 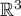 dans
dans  dont la matrice dans leur base
canonique respective est
dont la matrice dans leur base
canonique respective est
![\[A=\lp\begin{array}{ccc} 2&-1&1\\ 3&2&-3\enar\rp.\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2/4.png)
On appelle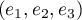 la base canonique de
la base canonique de  et
et 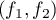 celle de
celle de  .
.
On pose
![\[e_1'=e_2+e_3,\ e_2'=e_3+e_1,\ e_3'=e_1+e_2\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2/9.png)
et
![\[f_1'=\dfrac12(f_1+f_2),\ f_2'=\dfrac12(f_1-f_2)\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2/10.png)
On appelle
On pose
et
- Montrer que
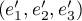 est une base de
est une base de 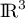 puis que
puis que  est une base de
est une base de 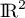 .
.
- Quelle est la matrice de
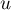 dans ces nouvelles bases?
dans ces nouvelles bases?
Correction
Correction
- Dans chaque cas, le nombre de vecteurs est égal
à la dimension de l'espace, et il suffit donc de montrer que ces deux familles sont libres.
Les vecteurs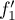 et
et 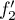 ne sont pas colinéaires,
donc la famille est libre.
ne sont pas colinéaires,
donc la famille est libre.
Pour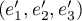 , soit
, soit 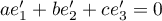 , alors on
, alors on
![\[\begin{array}{ll}(b+c)e_1+(a+c)e_2+(a+b)e_3=0
&\iff\la\begin{array}{rcl}b+c&=&0\\a+c&=&0\\a+b&=&0\enar\right.\\[2em]
&\iff a=b=c=0.\enar\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2_c/5.png)
et donc, la famille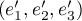 est libre et donc une base de
est libre et donc une base de 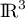 .
.
- Notons
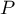 la matrice de passage de
la matrice de passage de 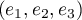 à
à 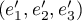 et
et 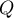 la matrice de passage de
la matrice de passage de 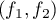 à
à 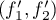 .
Alors on a :
.
Alors on a :
![\[P=\lp\begin{array}{ccc}0&1&1\\1&0&1\\1&1&0\enar\rp\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2_c/14.png)
et
![\[Q=\frac{1}{2}\lp\begin{array}{cc}1&1\\1&-1\enar\rp\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2_c/15.png)
Si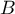 est la matrice de
est la matrice de 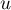 dans les nouvelles bases,
alors la formule du changement de base
nous dit que
dans les nouvelles bases,
alors la formule du changement de base
nous dit que 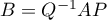 . Or,
. Or,
![\[Q^{-1}=\lp\begin{array}{cc}1&1\\1&-1\enar\rp\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2_c/19.png)
de sorte que
![\[B=\lp\begin{array}{ccc}-1&3&6\\1&3&-4\enar\rp\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2_c/20.png)
Tags:Applications linéairesMatricesEspace vectoriel
Autres sujets au hasard:

Voir aussi: