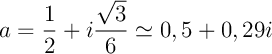Courbe de De Rham
Exemple d'IFS
Programmation et représentation de courbes de De Rham
Les courbes de De Rham sont un ensemble de courbe aux propriétés fractales.Les courbes de Koch, de Lévy et de Cesàro sont des cas particuliers de l'ensemble des courbes de de Rham.
Dans le cas où la courbe de de Rham est continue, elle est l'attracteur d'un IFS dont les fonctions sont données ci-dessous.
La programmation et représentation suivante utilise le jeu du chaos.
Courbe de De Rham
| Courbe de Cesàro | Cesàro |
| Lévy (-Cesàro) | |
| Courbes de Koch-Peano | Koch |
| Koch-Peano (1) | |
| Koch-Peano (2) |
a=α+iβ
=
+i
Construction des courbes de De Rham
Les courbes de De Rham sont définies à partir de deux fonctions contractantes d0 et d1. Plus précisément, les courbes de De Rham sont les ensembles des points fixes de fonctions composées de ces deux fonctions: d0, d1, d0∘ d0, d0∘ d1, d0∘ d0∘ d0 , d1∘ d0∘ d0 , …Le jeu du chaos permet aussi de construire ces courbes. On peut s'en convaincre et le montrer en montrant que dans une suite aléatoire infinie se trouve forcément toute suite finie.
Ainsi en utilisant successivement et aléatoirement d0 et d1, on utilise aussi, pour un nombre d'itérations assez important, les compositions finies adéquates.
Plus précisément le jeu du chaos ou IFS converge vers la courbe de De Rham lorsque la courbe concernée est continue (ce qui n'est pas toujours le cas, en se rappelant aussi que lorsque cette courbe est continue elle n'est pas, en général, dérivable).
Fonctions de l'IFS
Suivant les fonctions d0 et d1 on peut obtenir plusieurs catégories de courbes de de Rham.Courbe de Cesàro
Les courbes de Cesàro sont définies par des transformations affines directes (qui conservent l'oientation):![\[\la\begin{array}{l}
d_0(z)=az\\[.5em]
d_1(z)=a+(1-a)z
\enar\right.\]](IMG/1.png)
avec
![\[\la\begin{array}{ll}
d_0(z)&=(\alpha+i\beta)(x+iy)\\[.8em]
&=\bigl(\alpha x-\beta y\bigr) +i\bigl(\beta x+\alpha y \bigr)
\\[.8em]
d_1(z)&=\alpha +i\beta +(1-\alpha-i\beta)(x+iy)\\[.8em]
&=\bigl(\alpha +(1-\alpha)x +\beta y \bigr)
+i\bigl( \beta+(1-\alpha)y-\beta x \bigr)
\enar\right.\]](IMG/4.png)
La courbe de Lévy (ou courbe en C de Lévy) s'obtient avec le paramètre
Courbe de Koch-Peano
En utilisant des transformations affines indirectes (qui inversent l'orientation), on obtient les courbes de Koch-Peano, dont la célèbre courbe de Koch (ou fractale de Koch, ou flocon de Koch) est un cas particulier.![\[\la\begin{array}{l}
d_1(z)=a\overline{z}\\[.5em]
d_2(z)=a+(1-a)\overline{z}
\enar\right.\]](IMG/6.png)
avec
![\[\la\begin{array}{ll}
d_1(z)&=(\alpha+i\beta)(x-iy)\\[.8em]
&=\bigl(\alpha x+\beta y\bigr) +i\bigl(\beta x-\alpha y \bigr)
\\[.8em]
d_2(z)&=\alpha +i\beta +(1-\alpha-i\beta)(x-iy)\\[.8em]
&=\bigl(\alpha +(1-\alpha)x -\beta y \bigr)
+i\bigl( \beta-(1-\alpha)y-\beta x \bigr)
\enar\right.\]](IMG/9.png)
La courbe de Koch s'obtient avec le paramètre