IFS, fractales & jeu du chaos
Jeu du chaos
Principe, fonctionnement et algorithme
Le jeu du chaos, introduit initialement par Michael Barnsley dans les années 90 (du 20ème siècle), est un algorithme qui permet de générer l'attracteur d'un IFS, donc de générer des fractales, simplement et rapidement.
Comme pour l'algorithme IFS précédent, on part d'un point
Avec un IFS constitué de
Algorithme
M est un point au hasard
Pour i de 1 à n
p est un nombre entier aléatoire entre 1 et N
M=fp(M)
Dessiner M
Fin
où
n désigne le nombre d'itérations de notre système de fonctions.
Cet algorithme est plus simple à mettre en œuvre, mais la convergence vers l'attracteur est moins évidente.
En Python par exemple, le programme peut ressembler à: Programme Python
from random import random
M(,y) est un point au hasard
def f(i,x,y):
# definition de i-ème fonction
# de l'IFS
return [x,y]
for i in range(n):
r=random ()
if (r<1.0/N) {M=f(1,x,y)}
elif (r<2.0/N) {M=f(2,x,y)}
elif ...
else {M=f(N,x,y)}
Point(M[i]) # Trace le point avec libxy
Convergence
On peut démontrer la convergence du jeu du chaos, c'est-à-dire que l'ensemble des points construits ainsi converge vers l'ensemble des points de l'attracteur de l'IFS.
Évitant beaucoup d'éléments techniques, on peut se convaincre de cette convergence à l'aide la propriété suivante:
Propriété:
Toute suite aléatoire infinie contient
toute suite finie.
En effet, à la n-ième itération de l'algorithme IFS, les points obtenus sont des composés des fonctions
Ainsi, le jeu du chaos permet de produire la n-ième itération de l'algorithme IFS, pour tout entier
Il est plus dur par contre de préciser la vitesse de convergence du jeu du chaos, mais la pratique joue ici en faveur du jeu… du chaos.
On commence par démontrer un corollaire de la propriété.
Corollaire:
Toute suite aléatoire infinie contient une infinité de fois toute suite finie.
Démonstration du corollaire:
Soit 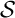 une suite aléatoire infinie et
une suite aléatoire infinie et 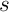 une suite donnée finie.
une suite donnée finie.
Alors, d'après la propriété précédente, est contenue dans
est contenue dans  ,
mais alors,
,
mais alors, 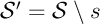 (la suite
(la suite  à laquelle on retire
à laquelle on retire 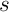 )
est aussi une suite aléatoire infinie.
Donc
)
est aussi une suite aléatoire infinie.
Donc  contient aussi
contient aussi 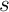 , etc …
, etc …
Alors, d'après la propriété précédente,
Démonstration de la propriété:
pour simplifier, on considère une suite binaire infinie aléatoire
 (une suite infinie de résultat de Pile: "0" ou Face: "1", par exemple).
(une suite infinie de résultat de Pile: "0" ou Face: "1", par exemple).
L'idée est de démontrer la propriété par l'absurde: si on suppose en effet qu'une suite finie, par exemple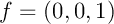 n'est pas contenu dans la suite
n'est pas contenu dans la suite 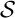 ,
alors, à chaque fois que l'on trouve la succession de deux zéros
dans
,
alors, à chaque fois que l'on trouve la succession de deux zéros
dans  on doit forcément trouver un zéro aussi suivant, pas de 1 qui donnerait
on doit forcément trouver un zéro aussi suivant, pas de 1 qui donnerait 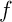 .
.
Ceci contredit le caractère l'aléatoire de la suite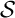 .
.
Encore faut-il s'assurer que l'on trouve une suite de deux zéros dans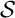 …
…
On démontre donc cette propriété par récurrence.
Pour une suite finie à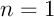 élément,
élément,  ou
ou 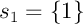 ,
la suite aléatoire infinie contient trivialement ces deux suites finies.
,
la suite aléatoire infinie contient trivialement ces deux suites finies.
Soit une suite finie de deux éléments: par exemple.
Supposons que
par exemple.
Supposons que 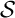 ne contienne pas
ne contienne pas 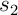 .
Alors, dans
.
Alors, dans 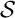 à chaque 0 rencontré suit nécessairement un autre 0,
sinon, avec un 1, on aurait
à chaque 0 rencontré suit nécessairement un autre 0,
sinon, avec un 1, on aurait  . Ceci contredit le fait que
. Ceci contredit le fait que
 soit aléatoire.
soit aléatoire.
Supposons maintenant que contienne toutes les suites finies de
contienne toutes les suites finies de
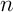 éléments, et considérons une suite
éléments, et considérons une suite  de
de
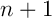 éléments.
éléments.
Alors pour une certaine suite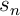 de
de 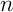 éléments,
éléments,
 par exemple
(ou
par exemple
(ou 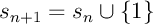 ).
).
D'après le corollaire,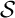 contient une infinité de fois
la suite
contient une infinité de fois
la suite 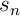 , et à chaque fois donc, le terme suivant devrait être
un 1.
Ceci contredit à nouveau l'aléatoire le caractère aléatoire de la suite
, et à chaque fois donc, le terme suivant devrait être
un 1.
Ceci contredit à nouveau l'aléatoire le caractère aléatoire de la suite
 .
.
L'idée est de démontrer la propriété par l'absurde: si on suppose en effet qu'une suite finie, par exemple
Ceci contredit le caractère l'aléatoire de la suite
Encore faut-il s'assurer que l'on trouve une suite de deux zéros dans
On démontre donc cette propriété par récurrence.
Pour une suite finie à
Soit une suite finie de deux éléments:
Supposons maintenant que
Alors pour une certaine suite
D'après le corollaire,
Systèmes dynamiques, théorie et jeu du chaos
La théorie du chaos est un domaine mathématique qui s'intéresse au comportement de systèmes dynamiques, c'est-à-dire de systèmes munis d'une loi d'évolution (souvent de l'évolution au cours du temps).
Pour des systèmes discrets, ou systèmes continus discrétisés, dans lesquels on peut utiliser une variable
En ce sens, un IFS fournit une loi d'évolution d'un système dynamique avec la suite d'ensembles
Les systèmes dynamiques chaotiques, étudiés et décrits dans ce qui porte le nom mathématique de "théorie du chaos", forment une classe de systèmes dynamiques particuliers caractérisés entre autre par une grande sensiblité aux conditions initiales: deux points de départs très proches peuvent aboutir après un certain nombre d'itération à deux états du système très différents.
Certains de ces systèmes permettent de générer des figures fractales en séparant en deux les points du plan: ceux pour lesquels le système dynamique diverge et les autres. Cette méthode permet de générer par exemple les ensembles fractals de Mandelbrot et de Julia.
Le jeu du chaos joue d'une certaine façon avec cette structure fractale chaotique: sous les conditions usuelles exposées (fonctions
Au contraire aussi des méthodes itératives permettant de calculer les états successifs d'un système dynamique déterministe, "le jeu du chaos" repose sur une méthode aléatoire.
On se joue d'une certaine façon du déterminisme, pour converger vers un état limite chaotique.
Jeu du chaos modifié - Règles de jeu
L'algorithme du jeu du chaos, dans sa simplicité, permet aussi d'ajouter des règles de construction simple, en influant par exemple sur l'aléatoire.
Par exemple, pour le jeu du chaos dans un polygone, on peut imposer qu'un sommet ne soit pas choisi deux fois consécutivement, ou encore que le sommet choisi ne soit pas "trop éloigné" du précédent, ou encore qu'une zone précise soit interdite.