Courbe de Lévy

Exemple d'IFS

La courbe de Lévy, ou encore courbe en C, ou aussi courbe du crabe, est une courbe fractale.

Description mathématique / Fonctions de l'IFS

La courbe de Lévy est l'attracteur de l'IFS défini par les deux fonctions

de $\R^2$ dans lui-même,

$f_1(x,y)=\left( \dfrac{x-y}{2},\dfrac{x+y}{2}\rp$

$f_2(x,y)=\left( \dfrac{x+y}{2}+\dfrac12,-\dfrac{x-y}{2}+\dfrac12\rp$

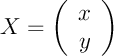Matriciellement, on peut les écrire, pour $X=\lp\begin{array}{c}x\\y\enar\rp$ ,

, où

$A_1=\dfrac12\lp\begin{array}{cc}1 & -1 \\ 1 & 1\enar\right) =\dfrac{1}{\sqrt2}\lp\begin{array}{cc} \cos\alpha_1 & -\sin\alpha_1 \\[1em] \sin\alpha_1 & \cos\alpha_1 \enar\right)$

$A_2=\dfrac12\lp\begin{array}{cc}1 & 1 \\ -1 & 1\enar\right) =\dfrac{1}{\sqrt2}\lp\begin{array}{cc} \cos\alpha_2 & -\sin\alpha_2 \\[1em] \sin\alpha_2 & \cos\alpha_2 \enar\right)$

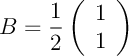avec $\alpha_1=\dfrac\pi4$ et $\alpha_2=-\alpha=-\dfrac\pi4$ , et $B=\dfrac12\lp\begin{array}{c}1\\1\enar\rp$ .
Les matrices

sont les matrices des similitudes d'angles $\alpha_1$ et $\alpha_2$ et de rapport $\dfrac1{\sqrt2}$ .

Courbe de De Rham

La courbe de Lévy peut aussi être vue comme un cas particulier de courde de De Rham. Ces courbes sont définies à partir des transformations complexes,

$\la\begin{array}{l} d_0(z)=az\\[.5em] d_1(z)=a+(1-a)z \enar\right.$

ou encore, dans le plan réeel, avec $a=\alpha+i\beta$ et

$\la\begin{array}{ll} d_0(z)&=(\alpha+i\beta)(x+iy)\\[.8em] &=\bigl(\alpha x-\beta y\bigr) +i\bigl(\beta x+\alpha y \bigr) \\[.8em] d_1(z)&=\alpha +i\beta +(1-\alpha-i\beta)(x+iy)\\[.8em] &=\bigl(\alpha +(1-\alpha)x +\beta y \bigr) +i\bigl( \beta+(1-\alpha)y-\beta x \bigr) \enar\right.$

avec $a=\dfrac12+\dfrac12i$

Variation: courbe de Lévy en sinus

On peut modifier par exemple la deuxième fonction en utilisant un sinus:

$f_2(x,y)=\lp\sin\lp\dfrac{x+y}{2}+\dfrac12\rp,\sin\lp-\dfrac{x-y}{2}+\dfrac12\rp\rp$

Variationd'un IFS

Plus généralement, toute fonction

contractante permet de faire une variation d'un IFS, en composant

avec une, ou plusieurs, fonction de l'IFS.
Précédemment, on a utilisé la fontion $V(x,y)=\left( \sin x,\sin y\rp$ , composée avec la deuxième fonction de l'IFS.