Un bref QCM

Exercice corrigé - Spécialité maths, première générale

Énoncé

Pour chacune des questions, une seule des trois réponses proposées est correcte. Une réponse exacte et justifiée rapporte un point et une mauvaise réponse enlève un demi-point. L'absence de réponse ne rapporte et n'enlève aucun point. Si le total est négatif, la note est ramenée à 0.

L'ensemble des solutions de l'équation est:

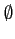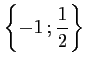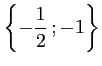
a) $\emptyset$ b) $\displaystyle \left\{-1\,;\dfrac{1}{2}\right\}$ c) $\displaystyle \left\{-\dfrac{1}{2}\,;-1\right\}$
L'ensemble de définition de la fonction 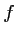telle que 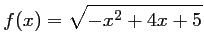$\displaystyle f(x)=\sqrt{-x^2+4x+5}$ est:

a) $\left[-1;5\right]$ b) $]-\infty;-1[\cup]5;+\infty[$ c)

Correction

1.

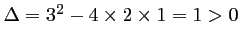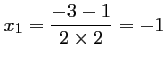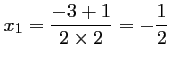Le discriminant de ce trinôme du second degré est $\Delta=3^2-4\times 2\times 1=1>0$ . L'équation admet donc deux solutions réelles distinctes: $\displaystyle x_1=\frac{-3-1}{2\times 2}=-1$ et $\displaystyle x_1=\frac{-3+1}{2\times 2}=-\frac{1}{2}$ , soit la réponse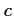

2.

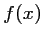est défini pour des valeurs de

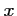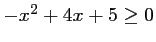telles que $-x^2+4x+5\geq 0$ .

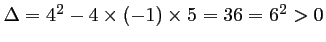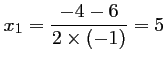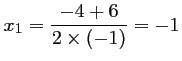Le discriminant de ce trinôme du second degré est $\Delta=4^2-4\times (-1)\times 5=36=6^2>0$ . Ce trinôme admet donc deux racines réelles distinctes: $\displaystyle x_1=\frac{-4-6}{2\times (-1)}=5$ et $\displaystyle x_1=\frac{-4+6}{2\times (-1)}=-1$ . Enfin, ce trinôme est positif, donc du signe de 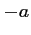, à l'intérieur de ses racines, soit sur l'intervalle , soit la réponse .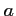

Tag:2nd degré

Autres sujets au hasard:

Voir aussi: