Polynôme de degré 3 et fraction rationnelle
Exercice corrigé - Spécialité maths, première générale
Énoncé
- Soit le polynôme
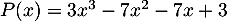 .
.
Vérifier que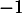 est une racine de
est une racine de 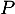 puis factoriser le polynôme sous la forme
puis factoriser le polynôme sous la forme
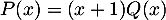 ,
où
,
où 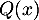 est un trinôme du second degré que l'on déterminera.
est un trinôme du second degré que l'on déterminera.
Résoudre alors l'équation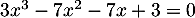 .
.
- On considère la fraction rationnelle :
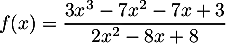
Résoudre l'inéquation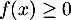 .
.
Correction
Correction
-
On a
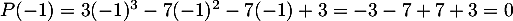 , ce qui montre que
, ce qui montre que 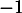 est bien une racine de
est bien une racine de 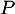 .
.
On en déduit que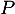 se factorise par
se factorise par 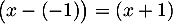 .
Soit donc
.
Soit donc 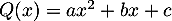 , alors on a:
, alors on a:
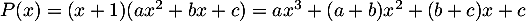 , d'où on déduit que
, d'où on déduit que
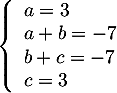 ,
soit donc,
,
soit donc,
 ,
, 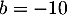 et
et 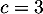 .
.
Ainsi,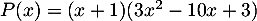 .
Le discriminant de
.
Le discriminant de 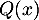 est
est
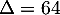 et ses racines sont
et ses racines sont 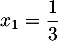 et
et 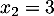 .
.
Les solutions de l'équation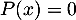 sont donc:
sont donc:
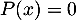 .
.
-
Le trinôme du dénominateur a pour discriminant
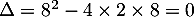 et admet donc un unique racine
et admet donc un unique racine 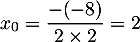 .
.
À l'aide de la factorisation obtenue au , on a
, on a
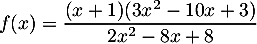 et les signes
et les signes
![\[
\begin{tabular}{|c|lcccccccccr|}\hline
$x$ & $-\infty$ & &$-1$& &$\frac{1}{3}$& &$2$& &$3$& &$+\infty$ \\\hline
$x+1$& &-& \zb&+& $|$ &+&$|$&+&$|$&+&\\\hline
$3x^2-10x+3$& &+& $|$&+& \mbox{$0\hspace{-0.67em}\mid$} &-&$|$&-&\mbox{$0\hspace{-0.67em}\mid$}&+&\\\hline
$2x^2-8x+8$& &+& $|$&+& $|$ &+&\zb&+&$|$&+& \\\hline
$f(x)$& &-& \zb&+& \zb &-&\db&-&\zb&+& \\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap1/ex2_c/23.png)
On a alors,![$f(x)\geq0 \Longleftrightarrow x\in[-1;\frac{1}{3}]\cup[3;+\infty[$](/Generateur-Devoirs/1S/Chap1/ex2_c/24.png)
Tag:2nd degré
Voir aussi:
