Devoir de maths corrigé, Graphes et chaînes de Markov
Terminale générale, mathématiques expertes
Devoir de mathématiques, et corrigé, posé en maths expertes, terminale générale, année scolaire 2023/2024
Exercice 1: Traffic aérien entre 4 villes
On considère quatre villes 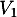 ,
, 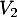 ,
, 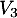 et
et 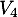 et le traffic aérien qui permet de relier ces quatre villes: il existe seulement des vols directs
et le traffic aérien qui permet de relier ces quatre villes: il existe seulement des vols directs
Cacher la correction
- de
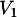 vers
vers 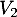 et de
et de 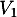 vers
vers 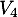 ,
,
- de
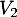 vers
vers 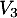 ,
,
- de
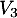 vers
vers 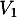 et de
et de 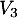 vers
vers 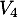 ,
,
- de
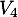 vers
vers 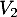
- Recopier et compléter le graphe suivant.
{$V_2$}
\rput(3,0){$\bullet$}\rput[l](3.2,0){$V_4$}
\rput(0,-3){$\bullet$}\rput(0,-3.3){$V_3$}
\psarc{<-}(0,0){3}{5}{85}
\psarc{->}(0,0){3}{95}{175}
\end{pspicture}\]](/Generateur-Devoirs/Mex/markov/extraffic/17.png)
- Écrire la matrice
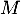 associée à ce graphe, en prenant les villes dans leur ordre de numération.
associée à ce graphe, en prenant les villes dans leur ordre de numération.
- Donner les matrices
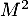 ,
, 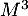 et
et 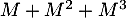 .
.
- Combien de vols comportant au plus deux escales permettent de relier
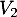 à
à 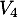 ?
?
- Existe t-il au moins un vol de chaque ville
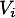 vers chaque ville
vers chaque ville 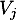 comportant au plus deux escales ? Pourquoi ?
comportant au plus deux escales ? Pourquoi ?
Correction exercice 1
-
{$V_2$}
\rput(3,0){$\bullet$}\rput[l](3.2,0){$V_4$}
\rput(0,-3){$\bullet$}\rput(0,-3.3){$V_3$}
\psarc{<-}(0,0){3}{5}{85}
\psarc{->}(0,0){3}{95}{175}
%
\psarc{->}(0,0){3}{185}{265}
\psarc{->}(0,0){3}{275}{355}
\psarc{->}(-3,0){4.3}{318}{42}
\psarc{->}(0,-3.2){4.3}{50}{131}
\end{pspicture}\]](/Generateur-Devoirs/Mex/markov/extraffic_c/1.png)
- La matrice associée à ce graphe est
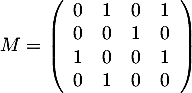 .
.
On a ensuite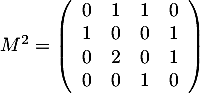 .
et
.
et
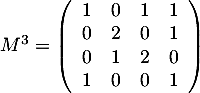 .
et donc
.
et donc
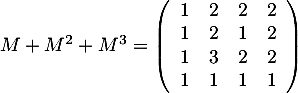 .
.
- La matrice d'adjacence
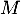 contient les vols directs entre les villes,
contient les vols directs entre les villes, 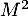 contient les nombres de vols avec exactement une escale, et
contient les nombres de vols avec exactement une escale, et 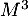 les nombres de vols avec exactement 2 escales.
les nombres de vols avec exactement 2 escales.
On trouve ainsi, dans la matrice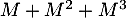 qu'il y a 2 vols avec au plus deux escales qui permettent de relier
qu'il y a 2 vols avec au plus deux escales qui permettent de relier 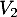 à
à 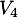 .
.
- Comme la matrice
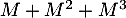 ne contient aucun zéro, toute ville
ne contient aucun zéro, toute ville 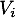 peut être reliée à chaque ville
peut être reliée à chaque ville 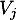 avec au plus deux escales.
avec au plus deux escales.
Cacher la correction
Exercice 2: Calcul d'un état stable
On considère une chaîne de Markov 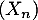 dans l'espace des états
dans l'espace des états 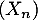 , dont la matrice
, dont la matrice 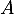 de transition associée est
de transition associée est
![\[A=\lp\begin{array}{cc}0,1&0,9\\0,4&0,6\enar\rp\]](/Generateur-Devoirs/Mex/markov/exetatstable/4.png)
On note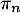 la distribution à l'étape des états à l'étape
la distribution à l'étape des états à l'étape 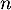 .
Initialement
.
Initialement 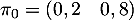 .
.
Cacher la correction
On note
- Déterminer
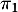 ,
, 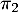 et
et 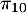 .
.
- Déterminer les éventuels états stables (ou distributions invariantes).
Correction exercice 2
-
![\[\begin{array}{ll}\pi_1&=\pi_0A\\&=\left( 0,2 \quad 0,8\rp\left(\begin{array}{cc}0,1&0,9\\0,4&0,6\enar\rp\\
&=( 0,34 \quad 0,66 )\enar\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/1.png)
puis, éventuellement à l'aide d'une calculatrice
![\[\pi_2=\pi_1A=( 0,298 \quad 0,702)\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/2.png)
puis
![\[\pi_{10}=\pi_0A^{10}\simeq( 0,3077 \quad 0,6923)\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/3.png)
- Un dstribution stable, ou invariante, est
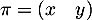 avec
avec 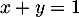 et
et
![\[\begin{array}{ll}\pi A= \pi
&\iff
\la\begin{array}{lclcl}
0,1x&+&0,4y&=&x\\
0,9x&+&0,6y&=&y\enar\right.\\[1.3em]
&\iff
\la\begin{array}{lclcl}
-0,9x&+&0,4y&=&0\\
0,9x&-&0,4y&=&0\enar\right.
\enar\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/6.png)
Ces deux équations sont équivalentes (l'opposée l'une de l'autre), et équivalente à
![\[x=\dfrac{0,4}{0,9}y=\dfrac49y\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/7.png)
Comme de plus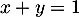 , on a donc
, on a donc
![\[x+y=\dfrac49y+y=\dfrac{13}9y=1\iff y=\dfrac9{13}\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/9.png)
On trouve alors aussi
![\[x+y=1 \iff x=1-y=\dfrac4{13}\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/10.png)
La seule distribution invariante est donc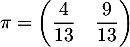
Cacher la correction
Exercice 3: Equilibre de gaz entre deux réservoirs
Deux compartiments, A et B, contiennent un gaz. Ces deux compartiments sont reliés entre eux, et le gaz peut donc librement passer d'un compartiment à l'autre.
Initialement le compartement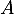 contient 10% du gaz et les 90% restants sont dans le compartiment B.
contient 10% du gaz et les 90% restants sont dans le compartiment B.
À chaque seconde, 40% du gaz présent dans le compartiment A passe dans le compartiment B, et de même 40% du gaz dans le compartiment B passe dans le A. On note alors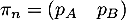 la répartition du gaz respectivement dans les compartiments A et B, au bout de
la répartition du gaz respectivement dans les compartiments A et B, au bout de 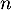 secondes.
secondes.
Cacher la correction
Initialement le compartement
À chaque seconde, 40% du gaz présent dans le compartiment A passe dans le compartiment B, et de même 40% du gaz dans le compartiment B passe dans le A. On note alors
- Représenter l'évolution de la proportion de gaz entre les deux compartiments par un graphe pondéré.
- La matrice de transition associée à ce graphe est
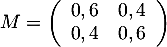 .
.
Donner la répartition du gaz au bout 1 seconde, puis au bout de 10 secondes.
- On considère la matrice
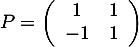 .
.
Montrer que cette matrice est inversible, puis que son inverse est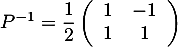 .
.
- Déterminer les nombres réels
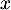 et
et 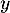 dans la matrice
dans la matrice 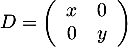 tel qu'on ait
tel qu'on ait
![\[M=PDP^{-1}\]](/Generateur-Devoirs/Mex/markov/exgaz/10.png)
- Calculer
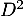 et donner, pour tout entier
et donner, pour tout entier 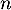 , la matrice
, la matrice 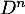 .
.
- Établir à l'aide d'un raisonnement par récurrence que, pour tout entier
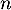 non nul, on a
non nul, on a 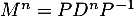 .
.
- Déterminer la limite
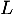 de la matrice
de la matrice 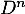 lorsque
lorsque 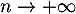 .
En déduire la distribution limite
.
En déduire la distribution limite 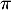 de la suite des distributions
de la suite des distributions 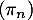 .
.
Correction exercice 3
-
![\[\psset{arrowsize=8pt}\begin{pspicture}(0,-.3)(4.5,2.)
%\psline{->}(1,1)(2.9,1)
\psarc{->}(.3,1){.6}{20}{335}
\psarc{->}(5.7,1){.6}{210}{160}
\psarc{<-}(3,0){2.2}{35}{145}
\psarc{<-}(3,2){2.2}{215}{325}
\rput(1,1){$\bullet$}\rput(.7,1){$A$}
\rput(5,1){$\bullet$}\rput(5.3,1){$B$}
%
\rput(-.65,1){0,6}
\rput(6.6,1){0,6}
\rput(3,1.9){0,4}
\rput(3,0){0,4}
\end{pspicture}\]](/Generateur-Devoirs/Mex/markov/exgaz_c/1.png)
- On a
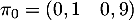 et au bout de 1s,
et au bout de 1s,
![\[\begin{array}{ll}\pi_1&=\pi_0M\\&=\left( 0,1 \quad 0,9\rp\left(\begin{array}{cc}0,4&0,6\\0,6&0,4\enar\rp\\
&\simeq( 0,42 \quad 0,58 )\enar\]](/Generateur-Devoirs/Mex/markov/exgaz_c/3.png)
Au bout de 10 secondes, la distribution est
![\[\pi_{10}=\pi_0M^{10}\simeq(0,5 \quad 0,5)\]](/Generateur-Devoirs/Mex/markov/exgaz_c/4.png)
à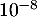 près.
près.
-
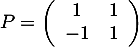 .
.
On a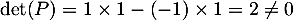 , ce qui montre que cette matrice est inversible.
, ce qui montre que cette matrice est inversible.
Ensuite, on calcule de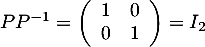 , ce qui montre que cette matrice
, ce qui montre que cette matrice 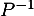 est bien la matrice inverse de
est bien la matrice inverse de 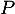 .
.
- On calcule
![\[\begin{array}{ll}
PDP^{-1}
&=\lp\begin{array}{cc}1&1\\-1&1\enar\rp\lp\begin{array}{cc}x&0\\0&y\enar\rp\dfrac12\lp\begin{array}{cc}1&-1\\1&1\enar\rp\\[1.3em]
&=\dfrac12\lp\begin{array}{cc}x&y\\-x&y\enar\rp\lp\begin{array}{cc}1&-1\\1&1\enar\rp\\[1.3em]
&=\dfrac12\lp\begin{array}{cc}x+y&-x+y\\-x+y&x+y\enar\right)
\enar\]](/Generateur-Devoirs/Mex/markov/exgaz_c/11.png)
Ainsi, pour avoir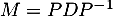 , on doit avoir
, on doit avoir
![\[\la\begin{array}{lcrcr}
\dfrac12(\ x+y)&=&0,6\\[1em]
\dfrac12(-x+y)&=&0,4
\enar\right.\]](/Generateur-Devoirs/Mex/markov/exgaz_c/13.png)
soit encore
![\[\la\begin{array}{rclcl}
x&+&y&=&1,2\\[1em]
-x&+&y&=&0,8
\enar\right.\]](/Generateur-Devoirs/Mex/markov/exgaz_c/14.png)
et donc, en ajoutant les deux équations, on obtient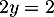 soit
soit 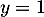 et de même, en les soustrayant, on obtient
et de même, en les soustrayant, on obtient
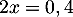 soit
soit 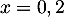
On trouve donc la matrice diagonale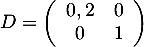
- On calcule facilement
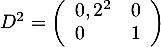 et plus généralement,
et plus généralement,
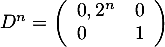 pour tout entier
pour tout entier 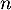 .
.
- Initialisation: pour
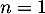 , on a
, on a 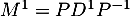 d'après le calcul de la question précédente.
d'après le calcul de la question précédente.
Hérédité: Supposons que, pour un entier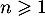 on ait
on ait 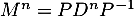 ,
,
alors,
![\[\begin{array}{ll}
M^{n+1}&=M^nM\\
&=PD^nP^{-1}M
\enar\]](/Generateur-Devoirs/Mex/markov/exgaz_c/27.png)
or on sait que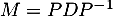 , d'où
, d'où
![\[\begin{array}{ll}
M^n&=PD^n\underbrace{P^{-1}P}_{=I_2}DP^{-1}\\[1.6em]
&=PD^nDP^{-1}\\[.6em]
&=PD^{n+1}P^{-1}
\enar\]](/Generateur-Devoirs/Mex/markov/exgaz_c/29.png)
ce qui montre que la formule est encore vraie au rang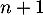 .
.
Conclusion: on vient donc de démontrer, d'après le principe de récurrence, que pour tout entier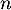 non nul,
non nul, 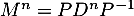 .
.
- Comme
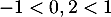 , on a
, on a 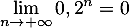 et alors,
et alors,
![\[\lim_{n\to+\infty}D^n=L=\lp\begin{array}{cc}0&0\\0&1\enar\rp\]](/Generateur-Devoirs/Mex/markov/exgaz_c/35.png)
Comme
![\[\pi_n=\pi_0M^n=\pi_0PD^nP^{-1}\]](/Generateur-Devoirs/Mex/markov/exgaz_c/36.png)
on en déduit que
![\[\lim_{n\to+\infty}\pi_n=\pi_0PLP^{-1}\]](/Generateur-Devoirs/Mex/markov/exgaz_c/37.png)
Il reste à faire les produits matriciels, et on trouve que
![\[\pi_0PLP^{-1}=( 0,5 \quad 0,5 )\]](/Generateur-Devoirs/Mex/markov/exgaz_c/38.png)
d'où la limite
![\[\lim_{n\to+\infty}\pi_n=( 0,5 \quad 0,5 )\]](/Generateur-Devoirs/Mex/markov/exgaz_c/39.png)
Après un temps assez long, le gaz s'équilibre exactement entre les deux compartiments: 50% dans chaque compartiment.
Cacher la correction
Quelques autres devoirs
sur les graphes et chaînes de Markov. Evolution probabiliste et états stables. Traffic aérien entre 4 villes et équilibre de gaz entre deux réservoirs
Quelques exercices corrigés
Exercices corrigés
Part de marché
Exercices corrigés
Répartition en deux opérateurs téléphoniques
Exercices corrigés
Traffic aérien entre 4 villes
Exercices corrigés
Recherche d'un etat stable
Exercices corrigés
Equilibre de gaz entre deux réservoirs
Voir aussi: