Graphes et chaînes de Markov



Introduction

Les chaînes de Markov sont des objets probabilistes qui permettent de modéliser assez simplement des situations dans lesquelles la prédiction de l'évolution future est dépendante de l'état présent, et exclusivement de l'état présent (dans indépendante du passé).
La mathématicien russe Andreï Markov, en publiant les premiers résultats dans ce domaine en 1906, laissa son nom à ces événements qui s'enchaînent.
Ce fut le début d'un domaine de recherche très riche et toujours d'actualité.
30 ans après les première publications de Markov, Kolmogorov généralisa les chaînes de Markov (en temps discret) en processus de Markov (en temps continu). Kolmogorov s'inspira certes des travaux de Markov, mais aussi des recherches et interrogations sur les fluctuations des marchés financiers et du modèle du mouvement Brownien introduit par Einstein (en 1905, la même année qu'il a publié ses deux articles révolutionnaires, l'un sur les quanta de lumière et l'autre sur la relativité)

On peut représenter efficacement une chaîne de Markov, ses états et probabilités de transition, par un graphe orienté et pondéré. Les états sont les sommets du graphe, les poids sur les arêtes sont les probabilités.
Ce chapitre commence ainsi par quelques paragraphes sur les graphes, et leurs représentations et exploitations matricielles. L'histoire des graphes débute au 18ème siècle à Königsberg avec Euler, voir l'exercice 1, et se poursuit encore de nos jours comme une branche des mathématiques discrètes et informatique.


Ce chapitre en mathématiques expertes en terminale générale apparaît comme une pierre angulaire, mêlant probabilités, matrices, graphes, suites et limites.

Pour aller plus loin, juste au delà des programmes de terminale et du lycée, les chaînes de Markov à temps continu permettent de modéliser des phénomènes dans lesquelles l'évolution n'est plus discrète (modélisée à l'aide de suite: étape 1, étape 2, … étape n, …) mais se fait à temps continu (pour tout t réel).
Dans cette variante des chaînes de Markov se mêlent alors aussi les fonctions (dont l'exponentielle), des probabilités continues, des intégrales. On modélise ainsi par exemple les phénomènes de file d'attente.


Échauffements, exercices & rappels

Exercice 1: Problème des 7 ponts de Königsberg
Le problème suivant, connu comme le problème des 7 ponts de Königsberg, fut résolu par Euler en 1735. Ce problème est de nos jours largement connu comme étant à l'origine de la théorie des graphes.
La ville de Königsberg (aujourd'hui Kaliningrad) est traversée par la rivière Pregolya, et comporte deux iles. Ces iles sont reliées entre elles et aux berges par, au total, 7 ponts.
Le problème est alors le suivant: est-il possible de se promener dans cette ville en passant une, et une seule, fois par tous les ponts ? Est-il possible de le faire à partir d'un point de départ au choix et de revenir finalement à son point de départ ? (bien sûr, on ne peut traverser la rivière qu'en empruntant un pont).

Correction
Ce problème historique est pris comme départ de la théorie des graphes.
On le trouve abondamment cité et documenté.
Voir là par exemple.

Exercice 2: arbre de probabilités
On considère une expérience aléatoire modélisée par l'arbre ci-contre.
  1. Compléter cet arbre.
  2. Déterminer P (A∩B) et P(B).
  3. Déterminer PA(B) et PB(A).

Correction
(Re)Voir les cours: Arbres et formules classiques de probabilités et Probabilités conditionnelles, indépendance et arbre de probabilité.
  2. P (A∩B) = 0,6×0,3 = 0,18
    et d'après la formule des probabilités totales,
    P(B) = 0,6×0,3 + 0,4×0,1 = 0,22
  3. PA(B) = P (A∩B)/P(A) = 0,18/0,6 = 0,3
    et
    PB(A) = P (A∩B)/P(B) = 0,18/0,22 ≃ 0,818

Exercice 3: système matriciel
Écrire le système suivant sous forme matriciel: 2x + y = 8 −3x + 4y = −1 puis le résoudre matriciellement.



Exercice 4: suite arithmético-géométrique
Soit la suite (un) définie par u0=7 puis par
un+1 = 0,5un+2
pour tout entier n.
  1. Vers quelle limite l la suite (un) peut-elle éventuellement converger ?
  2. On pose vn = un − 4.
    Montrer que (vn) est une suite géométrique dont on précisera la raison.
    Exprimer alors vn en fonction de n, puis un en fonction de n.
    Quelle est la limite de (un) ?



Exercice 5
Le glucose admet deux isomères (deux composés qui ont la même formule d'ensemble, mais un agencement différent des atomes dans la molécule et donc des propriétés différentes), le dextrose (qui est dextrogyre, c'est-à-dire qui a la propriété de dévier vers la gauche la lumière), et le lévulose (qui est lévogyre, c'est-à-dire qui dévie la lumière vers la droite).
Dans une certaine réaction chimique, dite de Pierre Landin, une partie du dextrose se transforme en lévulose et vice-versa. Plus précisément, au cours d'une unité de temps, 60% des molécules de dextrose se transforment en lévulose et les 40% restant demeurent sous forme dextrose, tandis que 35% des molécules de lévulose restent sous forme lévulose et que les 65% autres deviennent dextrose.
On note dn et ln les proportions de dextrose et de lévulose au temps n dans le mélange (l'unité de temps est l'heure). On suppose qu'on a, au départ, d0 = 1 et l0 = 0.
On note Un le vecteur colonne Un = dn ln
  1. Représenter l'évolution des proportions de dextrose et de levulose lors de cette réaction chimique par un graphe pondéré.
  2. Montrer alors que la réaction se traduit par une égalité matricielle de la forme Un+1 = AUn où A est une matrice 2x2 à préciser. En déduire qu'on a Un = AnU0
    3. .
  3. Calculer U1, U2, U3 et interpréter les résultats en termes de proportions de chaque composant.
  4. À l'aide de la calculatrice, calculer An pour n = 10, n = 20, n = 30.
    Que constate-t-on ? Qu'en déduit-on pour les proportions de dextrose et de lévulose ?
  5. On pose B = 0,520,52 0,480,48
    1. Calculer B2, B3, …, Bn
    2. Calculer C = 4(B−A), puis C2, C3, …, Cn.
    3. Calculer BC et CB.
    4. Déduire de ce qui précède la formule
      An = 0,52+0,48(−0,25)n0,52(1−(−0,25)n) 0,48(1−(−0,25)n)0,48+0,52(−0,25)n
    5. Calculer enfin dn et ln en fonction de n, et en déduire leurs limites lorsque n tend vers l'infini.



Graphes

Définitions - Terminologie des graphes

Définitions: Vocabulaire sur les graphes
  • Un graphe d'ordre n est un ensemble de n points, appelés sommets, relié entre eux par des liens.
  • Le graphe peut être non orienté, les liens reliant deux sommets se schématisent par un trait, ou arête.
    Le graphe peut aussi être orienté, les liens se schématisent alors par une flèche, aussi appelé arc.
    Dans ce cas un sommet peut aussi être relié à lui-même par une boucle.
  • Deux sommets sont adjacents s'ils sont reliés par une arête ou un arc.
  • Un sommet adjacent à aucun autre est dit isolé.
  • Le degré d'un sommet est le nombre d'arêtes ou d'arcs dont ce sommet est une extrémité (une boucle comptant pour 2)
  • Un graphe est complet si tous les sommets sont adjacents entre eux.

Exercice 6
Compléter:
  1. Un graphe non orienté d'ordre … :
    SommetABCDE
    Degré2
  2. Un graphe orienté d'ordre … :
    SommetABCDE
    Degré3

  1. C'est un graphe non orienté d'ordre 5 et
    SommetABCDE
    Degré23210
  2. C'est un graphe orienté d'ordre 5 et
    SommetABCDE
    Degré34311


Propriété
Dans un graphe, la somme des degrés de chaque sommet est égale au double du nombre d'arêtes

Définitions: Parcours dans un graphe
  • Une chaîne de longueur n est une liste de n sommets telle que chaque sommet de la liste soit adjacent au suivant.
  • Un graphe est connexe s'il existe une chaîne entre deux sommets quelconques de ce graphe.
    Pour un graphe orienté, on distingue:
    • fortement connexe: pour tout couple de sommets A et B, il existe un chemin de A à B et de B à A.
    • faiblement connexe: si le graphe est connexe sans considérer l'orientation des arcs.
  • Une chaîne est fermée lorsque l'origine et l'extrémité sont confondues.
  • Une chaîne fermée composée d'arêtes toutes distinctes s'appelle un cycle.


Exemples:
Dans le 1er graphe de l'exercice précédent, A-B-C et A-B-D-B-C sont des chaînes de longueurs 3 et 4.
C-B-D-B-A-C est une chaîne fermée.
A-B-C-A est un cycle de longueur 4.

Matrice d'adjacence



Définition: Matrices d'adjacence
À tout graphe G d'ordre n on associe une matrice carrée M = (mi,j) telle que mi,j = 1 si une arête ou un arc relie les sommets i et j, et mi,j = 0 sinon.
Cette matrice s'appelle la matrice d'adjacence du graphe G.

Exercice 7
Compléter les matrices d'adjacence:

  1. M = 011.. 10... ..000 ..... .....

  2. M = ...00 .01.. 010.. ..... 0....

  1. M = 01100 10110 11000 01000 00000
  2. M = 11000 00110 01001 00000 00000


Théorème: Nombre de chemin de longueur p
Soit un graphe G de matrice d'adjacence M = (mi,j).
On note Mp = ( mi,j(p) ). Le coefficient mi,j(p) de la matrice Mp est le nombre de chemins de longueur p reliant le sommet i au sommet j.

Exercice 8
Avec le graphe précédent,
dont la matrice d'adjacence est:
M = 11000 00110 01001 00000 00000
  1. On a
    M2 = 11110 01001 00110 00000 00000

    Il y a par exemple … chemin(s) de longueur … reliant B à B.
    Il y a par exemple … chemin(s) de longueur … reliant B à D.
  2. Calculer M3.
    Il y a ici par exemple … chemins de longueur … reliant A à B.
  3. M7 = 14333 00110 01001 00000 00000
    Il y a ici par exemple … chemins de longueur … reliant A à E.

  1. Il y a par exemple 1 chemin(s) de longueur 2 reliant B à B.
    Il y a par exemple 0 chemin(s) de longueur 2 reliant B à D.
  2. M3 = 12111 00110 01001 00000 00000

    Il y a par 2 chemins de longueur 3 reliant A à B.
  3. Il y a ici par exemple 3 chemins de longueur 7 reliant A à E.

Exercice 9
Les arêtes du graphe suivnat représentent des pistes de ski mesurant chacune 2km. Les sommets de ce graphes sont les différents points d'accès à ce domaine skiable.
  1. Donner la matrice d'adjacence du graphe.
  2. Déterminer le nombre de parcours de 4 km reliant A à C.
  3. Déterminer le nombre de parcours de 6 km reliant C à lui-même.
  4. Déterminer le nombre de parcours de 6 km reliant A à D.
  5. Déterminer le nombre de parcours d'au plus 8 km reliant A à D.

  1. La matrice d'adjacence du graphe est M = 1010 0011 1100 0010
  2. Pour compter le nombre de parcours de 4 km, donc en 2 arêtes, on utilise la matrice M2 = 0021 1110 0112 1100 Dans cette matrice, on trouve qu'on a 2 chemins de longueur 2, donc de 4 km, reliant A à C.
  3. Pour 6 km, donc des chemins de longueur 3, dans la matrice on calcule la matrice M3 = 2210 1212 1131 0112 On a là 3 chemins fermés de longueur 3, donc 6 km.
  4. Pour 6 km, donc des chemins de longueur 3, on a dans la matrice M3, on n'a aucun chemin reliant A à D.
  5. Il faut ajouter là les nombres de chemin dans les matrices M, M2, M3 et M4, reliant A à D.
    On calcule donc M4 = 1324 1243 3422 1131
    Il y a en tout: 0+1+0+4 = 5 chemins de longueur inférieure à 8 km

Graphe pondéré

Définition: Graphe pondéré
Un graphe, orienté ou non, est pondéré lorsque chacune des arêtes est affectée d'un poids: un nombre positif.

Exemple:
La chaîne A-B-C-B-D est une chaîne de poids 1+12+9+7 = 29

Exercice 10: Voyageur de commerce
On s'intéresse au problème dit "du voyageur de commerce": dans un ensemble de villes, trouver le plus court circuit passant par chaque ville une seule fois.
  1. On considère dans un premier temps un graphe complet de 5 villes: A, B, C, D et E.
    1. On exclut dans un premier temps le sommet E et on ne considère donc que le sous-graphe constitué des sommets A, B, C et D.
      Combien existe-t-il de chaînes fermées débutant et terminant en A, et ne passant qu'une seule fois par chaque autre sommet ?
      Comment trouver l'itinéraire le plus court ?
    2. Même question en prenant aussi en compte le sommet E.
    3. Combien de chaînes fermées peut-on faire en tout, en partant d'un sommet quelconque et terminant sur ce même sommet ?
  2. Combien de chaînes fermées peut-on faire dans un graphe complet avec 10 sommets (10 villes) ? 20 sommets ? 30 sommets ? 50 sommets ? 100 sommets ?
  3. En admettant que le calcul du poids total (ou distance totale) nécessite 1μs pour chaque itinéraire, quel est le temps de calcul nécessaire pour le calcul de tous les itinéraires possibles avec 10 sommets ? 20 sommets ? 30 sommets ? 50 sommets ?

    1. On peut s'aider d'un arbre.
      On part de A. Ensuite on a 3 possibilités: B, C ou D. À chacune de ces 3 possibilités, il en reste après 2, les deux villes restantes.
      Enfin il ne reste après plus qu'une ville à parcourir avant de revenir en A.
      En tout, il y a 3×2×1 = 6 possibilités.

      Pour trouver l'itinéraire le plus court, il suffit de calculer le poids (ou la longueur) de ces 6 possibilités, et de choisir la plus courte.
    2. Avec aussi le sommet E, on a tout d'abord, après A, 4 villes possibles: B, C, D ou E.
      À la 2ème ville, il reste alors 3 possibilités pour le choix de la 3ème ville.
      Enfin à la 3ème ville, il ne reste plus que 2 possibilités pour le choix de la 4ème ville.
      Enfin, la dernière ville à visiter avant de revenir en A s'impose d'elle-même.
      En tout il y a donc 4×3×2×1 = 24 possibilités.
    3. Si le sommet de départ est quelconque, on a alors 5 possibilités pour le choisir: A, B, C, D ou E.
      Une fois ce sommet de départ (et d'arrivé) choisi, on est de retour au calcul de la question précédente: pour chaque sommet =possible de départ, il y a ensuite 24 possibilités.
      En tout il y a donc 5×24 = 120 possibilités pour 5 sommets (5 villes).
  2. De même, dans un graphe complet avec 12 sommets, on peut construire
    10! = 10×9×…×2×1 = 3 628 800
    chemins fermés différents.
    Avec 20 sommets, on peut construire
    20! = 20×19×…×2×1 ≃ 2,4 1018
    chemins fermés différents, soit environ 2 milliards de milliards de chemins.
    Avec 30 sommets, on peut construire
    30! = 30×29×…×2×1 ≃ 2,6 1032
    chemins fermés différents, soit environ 200 000 milliards de milliards de milliards de chemins
    Avec 50 sommets, on en a
    50! = 50×49×…×2×1 ≃ 3 1064
    et enfin (pour les calculatrices capables de le calculer) pour 100 sommets
    100! = 100×99×…×2×1 ≃ 10158
  3. On a 1μs = 10−6s et donc:
    • pour 10 sommets, un temps de
      3 628 800×10−6s ≃ 3,6s
    • pour 20 sommets, un temps de
      2,4 1018×10−6s = 2,4 1012s
      soit, en convertissant en unités de temps plus parlantes, un temps de
      2,4 1012/3600×24×365≃76 000 ans
    • pour 30 sommets, un temps de
      2,6 1032×10−6/3600×24×365≃8 1018 ans
      soit environ 8 milliards de milliards d'années !! … pour seulements 30 villes …

Le calcul de l'itinéraire le plus court, pour un nombre important de sommets ne peut donc clairement pas se faire par une liste exhaustive de tous les itinéraires.
Dans ces graphes pondérés, l'algorithme de Moore-Dijkstra permet de déterminer la chaîne la plus courte reliant deux sommets de manière efficace.
Il permet de passer du O(n!) à du O(nln(n)).


Chaînes de Markov

Graphe probabiliste

Définition: Graphe probabiliste
Un graphe probabiliste est un graphe orienté et pondéré tel que:
  • Tous les poids sont positifs et inférieurs à 1: ce sont des probabilités
  • La somme des poids des chemins issus de chaque sommet est égale à 1.

La matrice d'adjacence d'un graphe probabiliste est une matrice stochastique: une matrice carrée avec des coefficients positifs dont la somme à chaque ligne est égale à 1.

Exercice 11
  1. Compléter la matrice d'adjacence M = 0,20,8. ... .0,4. du graphe suivant et vérifier qu'il s'agit d'une matrice stochastique.
  2. Un arbre pondéré peut être vu comme un graphe probabiliste, avec par exemple deux événements A et B, donc 4 états A, A, B et B:
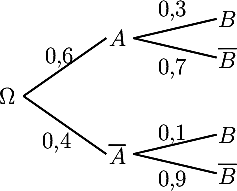
    Arbre pondéré des probabilités
    qui peut se représenter sous la forme: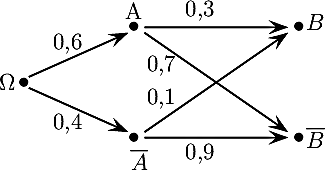
    abre pondéré comme un graphe

    Donner les probabilités PA(B), P(B), PB(A), PB(A), PB(A) et PB(A) et compléter les probabilités sur l'arbre inversé:


    Compléter alors finalement le graphe orienté complet et en donner la matrice d'adjacence:




Chaîne de Markov

Définition: Chaîne de Markov
Une chaîne de Markov est une suite de variables aléatoires (Xn) définies sur un même espace fini muni d'une probabilité et à valeur dans un ensemble E appelé espace d'états et vérifiant
P(X0=e0, X1=e1, … , Xn=en) (Xn+1=en+1) = P(Xn=en) (Xn+1=en+1)
En d'autres termes, la situation du système à l'instant n+1 ne dépend que de sa situation à l'instant n, et aucunement des situations antérieures X0, X1, … , Xn−1.

Exemples:
  • On considère une urne contenant 10 boules noires et 10 boules blanches dans laquelle on effectue successivement des tirages de la manière suivante: on tire tout d'abord une boule, puis au 2ème tirage on tire une autre boule et on remet celle tirée au 1er tirage. Au 3ème tirage on tire une boule et on remet celle tirée au 2ème, ...

    On note Xn la variable aléatoire égale à la couleur de la boule tirée au n-ième tirage. L'espace d'états est E = { "noire", "blanche" }
  • Météo probabiliste simpliste: un jour donné il peut faire beau, mauvais ou un temps variable.
    Lorsqu'un jour il fait beau, il y a une chance sur deux pour qu'il fasse encore beau le lendemain, et une chance sur dix qu'il fasse mauvais.
    S'il fait mauvais un jour, il y a aussi une chance sur deux pour que cela continue le lendemain, et une chance sur dix pour qu'il fasse beau.
    Enfin, lorsque le temps est variable un jour, il y a une chance sur cinq pour que le temps reste variable le lendemain, et autant de chance qu'il fasse beau ou mauvais.
    On note Xn la variable aléatoire égale au temps qu'il fait le n-ième jour.
    L'espace d'états est E = { "beau", "variable", "mauvais" }

On peut préciser un ensemble particulier et courant de chaîne de Markov:
Définition: Chaîne de Markov homogène
Une chaîne de Markov est dite homogène si, de plus, les probabilités P(Xn=i)(Xn+1=j) ne dépendent pas de n.
On note alors pi,j cette probabilité, et la matrice P = (pi,j) est appelée matrice de transition de la chaîne de Markov.

Remarque: Avec une modélisation par une chaîne homogène, la probabilité de passage à l'état j ne dépend donc que de l'état présent du système.
En particulier, P(Xn=j)(Xn+1=j) = P(X0=j)(X1=i)


Propriété
La matrice de transition P = (pi,j) d'une chaîne de Markov homogène est une matrice stochastique.
À une matrice d’une chaîne de Markov homogène, on peut associer un graphe probabiliste dont les sommets sont les états de l'espace d'état E et les arcs reliant l'état i à l'état j sont affectés des coefficients pi,j.



Propriété
On considère une chaîne de Markov homogène (Xn) dont on note P la matrice de transition associée et π0 la distribution initiale.
  • Si on note Pn = (pi,j(n)) alors on a
    pi,j(n) = P(X0=i)(Xn=j)
  • En notant πn la distribution de Xn, on a alors, pour tout entier n,
    πn+1 = πnP
    et donc, avec π0 la distribution initiale,
    πn = π0Pn

Remarque: Une chaîne de Markov homogène est donc entièrement déterminée par sa distribution initiale et par sa matrice de transition

Exercice 12
On considère une chaîne de Markov à trois états A, B et C, dont la matrice de transition est P = 0,200,8 0,10,30,6 0,50,50 .
La distribution initiale est π0 = (0,5   0,5   0).
  1. Donner les valeurs des probabilités P(X0=A), P(X0=C), P(X1=A) et P(X2=C).
  2. Exprimer πn en fonction de π0 et P.

  1. On a directement dans la matrice P(X0=A)= 0,5 et P(X0=C)= 0.
    Pour les probabilités de X1, on calcule la distribution π1 = π0P soit
    π1 = (0,5   0,5   0) 0,200,8 0,10,30,6 0,50,50 = (0,15   0,15   0,7)
    et donc P(X1=A)= 0,15.
    De même pour X2, on calcule la distribution
    π2 = π1P = (0,395   0,395   0,21)
    et on y trouve donc que P(X2=C)= 0,21.


Exercice 13
Dans une université, les étudiants participent à un mouvement de grève.
Le premier jour, 20% des étudiants faisaient grève.

On note Xn la variable aléatoire qui indique si un étudiant désigné au hasard dans l'université fait grève ou non le n-ième jour.
On admet que la suite (Xn) est une chaîne de Markov dont la matrice de transition est
P= 0,70,3 0,330,67
dans l'ordre grèviste, non grèviste. On note enfin πn la distribution le n-ième jour.
  1. Quelle est la probabilité qu'un étudiant qui fait grève un jour donné ne fasse plus grève le lendemain ? Quelle est la probabilité qu'un non grèviste un jour le reste le lendemain ?
  2. Donner π0, π1, et π2.
  3. Donner la probabilité qu'un étudiant soit en grève le 3ème jour.

  1. La probabilité qu'un étudiant qui fait grève un jour donné ne fasse plus grève le lendemain est de 0,3, et celle qu'un non grèviste un jour le reste le lendemain est de 0,67
  2. D'après l'énoncé, on a directement
    π0 = (0,2   0,8)

    On calcule ensuite la distribution π1 = π0P = (0,404   0,596) puis π2 = π1P ≃ (0,48   0,52)
  3. π0 est la distribution pour le 1er jour, π1 est la distribution pour le 2ème jour, et donc π2 est la distribution pour le 3ème jour, et donc, d'après le résultat précédent, la probabilité qu'un étudiant soit en grève le 3ème jour est de 0,48.


Distribution invariante

Définition: Distribution invariante d'une chaîne de Markov
Soit une chaîne de Markov homogène (Xn) de matrice de transition P.
Une distribution invariante est une matrice ligne π telle que: π P = π.

On parle aussi d'état stable de la chaîne de Markov.

Remarque: On a π P = π ⇔ π(In−P) = 0 avec In la matrice identité.
Le vecteur ligne nul est toujours solution de cette équation matricielle, mais le vecteur ligne n'est pas une distribution de probabilité (la somme de ses élements ne vaut pas 1).
Ainsi, si la matrice In−P est inversible, le système π(In−P)=0 admet une unique solution, qui est donc le vecteur nul, et il n'existe donc pas de distribution invariante.
Les distribution invariantes sont donc à rechercher lorsque la matrice In−P n'est pas inversible.

Exemple: Soit P = 01 10
On a alors I2−P = 1−1 −11 dont le déterminant vaut
det(I2−P) = 1×1−(−1)×(−1) = 0
Ainsi le système πP = π ⇔ π(I2−P) = 0 n'admet pas qu'une unique solution (pas que la solution nulle).
On vérifie que π = 1/2 1/2 est une distribution invariante.

Exercice 14
  1. Trouver deux nombres réels strictement positifs x et y tels que x+y = 1 et solutions du système: 2/3x + 1/6y = x 1/3x + 5/6y = y
  2. En déduire une distribution invariante de la chaîne de Markov définie par la matrice de transition P = 2/31/6 1/35/6

  1. En mettant tout du même côté, on a −1/3x + 1/6y = 0 1/3x − 1/6y = 0 Ces deux équations sont équivalentes (l'opposée l'une de l'autre), et on a donc
    1/3x −1/6y = 0 ⇔ 2x = y
    On a alors
    x+y=1 ⇔ 2x+x=1 ⇔ x = 1/3
    puis
    x+y=1 ⇔ y = 1−x = 2/3
  2. Une distribution π = (x   y) vérifie x+y=1 et de plus invariable donc π=πP.
    La solution est donc celle trouvée précédemment.

Exercice 15
On considère une chaîne de Markov dont la matrice de transition est P = 0,40,6 0,90,1
Déterminer une distribution π invariante.

On a π = (x   y), avec x+y = 1 et πP = π, soit le système d'équations 0,4x + 0,9y = x 0,6x + 0,1y = y soit aussi −0,6x + 0,9y = 0 0,6x − 0,9y = 0
On a deux équations équivalentes, et qui donnent x = 0,9/0,6y = 3/2y et, comme x+y =1 on a aussi
3/2y+y = 5/2y = 1
d'où y = 2/5 et alors
x = 1−y = 3/5
Ainsi, une distribution invariante est
π = (0,6   0,4)


Les distributions invariantes sont importantes dans l'étude d'une chaîne de Markov, en raison du théorème suivant:

Propriété
Soit (Xn) une chaîne de Markov homogène et (πn) la suite de ses distributions, alors si (πn) converge, (πn) converge vers une distribution invariante (théorème du point fixe pour les suites récurrentes).

Pour une chaîne de Markov à deux états, quelque soit la distribution initiales π0, la suite (πn) des distributions converge vers la distribution invariante π.

Exercice 16
On considère une chaîne de Markov (Xn) décrite par le graphe suivant et la distribution initiale π0 = (1   0).

  1. Écrire la matrice de transition $M$ associée à cette chaîne de Markov.
  2. Calculer π1 et π2.
  3. Donner l'expression de πn en fonction de n, puis calculer π5 et π10 (à l'aide de la calculatrice, un ordinateur, ...)
  4. Montrer que (Xn) admet une distribution invariante πl et la déterminer.

ddd

Exercice 17
On considère une chaîne de Markov à deux états A et B dans laquelle PA(B) = PB(A), avec PB(A) différent de 0 et de 1.
Montrer qu'à long terme, et quelque soit la distribution de probabilité initiale, les deux états sont équiprobables.



Exercices


Exercice 18
Les célèbres Dalton sont à l'heure actuelle en prison.
Chaque semaine, ils tentent de s'évader et leur tentative est une réussite une fois sur trois. Une fois évadés, ils ont chaque semaine trois chance sur quatre de se faire capturer.
  1. Modéliser cette situation par une chaîne de Markov à deux états.
    On notera L l'état "les Dalton sont libre" et P l'état "les Dalton sont en prison".
    Déterminer alors la probabilité qu'ils soient libre dans trois semaines.
  2. Quelle est la probabilité qu'ils purgent la totalité de leur peine d'un mois de prison (quatre semaines) sans avoir réussi à s'évader une seule fois ?


Exercice 19 (D'après Bac ES, Liban 2018)
Dans un pays deux opérateurs se partagent le marché des télécommunications mobiles. Une étude révèle que chaque année:
  • parmi les clients de l'opérateur EfficaceRéseau, 70% se réabonnent à ce même opérateur et 30% souscrivent un contrat avec l'opérateur GenialPhone;
  • parmi les clients de l'opérateur GenialPhone, 55% se réabonnent à ce même opérateur et 45% souscrivent un contrat avec l'opérateur Efficaceréseau.
On note E l'état: "la personne possède un contrat chez l'opérateur EfficaceRéseau" et G l'état: "la personne possède un contrat chez l'opérateur GenialPhone".
À partir de 2018, on choisit au hasard un client de l'un des deux opérateurs.

On note également:
  • en la probabilité que le client possède un contrat avec l'opérateur EfficaceRéseau au 1ier janvier (2018+n);
  • gn la probabilité que le client possède un contrat avec l'opérateur GenialPhone au 1ier janvier (2018+n);
  • Pn = (en &nsbp; gn) désigne la matrice ligne traduisant l'état probabiliste du système au 1ier janvier (2018+n)
Au 1er janvier 2018, on suppose que 10% des clients possèdent un contrat chez EfficaceRéseau, ainsi P0 = (0,1   0,9).
  1. Représenter cette situation par un graphe probabiliste de sommets E et G.
    1. Déterminer la matrice de transition M associée au graphe en rangeant les sommets dans l'ordre alphabétique.
    2. Vérifier qu'au 1ier janvier 2020, environ 57% des clients ont un contrat avec l'opérateur EfficaceRéseau.
    1. On rappelle que pour tout entier naturel n, Pn+1 = Pn×M.
      Exprimer en+1 en fonction de en et gn.
    2. En déduire que pour tout entier naturel n, en+1 = 0,25 en + 0,45
  4. Déterminer l'état stable du système et interpréter votre réponse dans le contexte de l'exercice.

\begin{enumerate} \item On représente cette situation par un graphe probabiliste de sommets $E$ et $G$: \[\psset{unit=1cm} \begin{pspicture}(-4.5,-0.8)(6,1.2) \Rnode{C}{$E$} \hskip 4cm \Rnode{T}{$G$}%définition des sommets \psset{nodesep=4pt,arcangle=15,arrowsize=2pt 3}% paramètres \ncarc{->}{C}{T} \Aput{0,30}% arc \ncarc{->}{T}{C} \Aput{0,45}% arc \nccircle[angleA=90]{->}{C}{4mm} \Bput{0,70}% boucle \nccircle[angleA=-90]{<-}{T}{.4cm} \Bput{0,55}% boucle \end{pspicture}\] \item \begin{enumerate} \item La matrice de transition est: $M = \begin{pmatrix} 0,70&0,30\\0,45&0,55\end{pmatrix}$. \item $P_2 = P_0 \times M^2 = (0,56875\quad 0,43125)$ donc $e_2\approx 0,57$ soit 57\,\%. \end{enumerate} \item \begin{enumerate} \item On rappelle que $P_{n+1} = P_n\times M$. Donc pour tout entier naturel $n$,\\ $(e_{n+1}\quad g_{n+1})= (e_{n}\quad g_{n}) \times \begin{pmatrix} 0,70&0,30\\0,45&0,55\end{pmatrix} = (0,70\times e_n+0,45\times g_n \quad 0,30\times e_n+0,55 \times g_n)$. Donc $e_{n+1}=0,70e_n+0,45g_n$. \item Pour tout entier naturel $n$, $e_n+g_n=1$ donc $g_n=1-e_n$.\\ Donc $e_{n+1}=0,70e_n+0,45(1-e_n)$ et donc $e_{n+1}=0,25e_n+0,45$. \end{enumerate} \item Pour trouver l'état stable $\begin{pmatrix} e & g \end{pmatrix}$ il suffit de résoudre le système d'équations:\\ $\left\{ \begin{array}{lc r} e&=&0,25e+0,45 \\ e+g &=& 1 \end{array}\right.$ La première équation donne : $0,75 e=0,45$ donc $e=\dfrac{0,45}{0,75}=0,6$. Donc $g=1-e=0,4$. L'état stable est donc $P = \begin{pmatrix} 0,6 & 0,4 \end{pmatrix}$. Ceci signifie qu'à partir d'un certain nombre d'années la part de marché de l'opérateur \emph{EfficaceRéseau} sera de 60\,\%. \end{enumerate}

Exercice 20: Marche aléatoire
Marche aléatoire} Un robot se déplace unidirectionnellement, vers la droite ou vers la gauche, au hasard et avec la même probabilité.
Il peut se trouver en trois position, A, B ou C et est bloqué par un mur sur la gauche de A. Depuis A, il peut donc, avec la même probabilité, se déplacer en B ou rebondir contre le mur et se retrouver à nouveau en A.
En C, le robot à chuté et ne peut, bien sûr, plus aller ailleurs qu'en C.
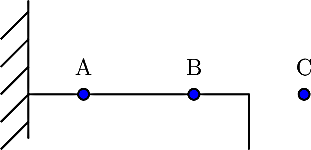
Schéma de la marche aléatoire du robot

Le robot est initialement en A.
Quelle est la probabilité qu'il ait chuté après 3 déplacements ? après 5 déplacements ? après 10 déplacements ?

On a une chaîne de Markov à 3 états A, B et C, et de matrice de transition
P = 0,50,50 0,500,5 001
On calcule alors
P3 ≃ 0,04690,03120,0781 0,031250,0156250,265625 001
puis
P5 ≃ 0,00780,00490,089 0,00490,00290,271 001
et enfin
P10 ≃ 5.10−65.10−59.10−2 5.10−53.10−50,273 001
En partant de A, la probabilité qu'il arrive en C (c'est-à-dire chute) au bout de 3 déplacements est environ 0,0781.
La probabilité qu'il chute après 5 déplacements est d'environ 0,089, et après 10 déplacements d'environ 0,09.



Voir aussi:
LongPage: h2: 5 - h3: 6