Recherche d'un etat stable
Exercice corrigé - Maths expertes, terminale générale
Énoncé
On considère une chaîne de Markov 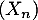 dans l'espace des états
dans l'espace des états 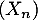 , dont la matrice
, dont la matrice 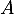 de transition associée est
de transition associée est
![\[A=\lp\begin{array}{cc}0,1&0,9\\0,4&0,6\enar\rp\]](/Generateur-Devoirs/Mex/markov/exetatstable/4.png)
On note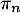 la distribution à l'étape des états à l'étape
la distribution à l'étape des états à l'étape 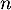 .
Initialement
.
Initialement 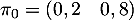 .
.
On note
- Déterminer
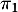 ,
, 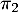 et
et 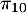 .
.
- Déterminer les éventuels états stables (ou distributions invariantes).
Correction
Correction
-
![\[\begin{array}{ll}\pi_1&=\pi_0A\\&=\left( 0,2 \quad 0,8\rp\left(\begin{array}{cc}0,1&0,9\\0,4&0,6\enar\rp\\
&=( 0,34 \quad 0,66 )\enar\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/1.png)
puis, éventuellement à l'aide d'une calculatrice
![\[\pi_2=\pi_1A=( 0,298 \quad 0,702)\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/2.png)
puis
![\[\pi_{10}=\pi_0A^{10}\simeq( 0,3077 \quad 0,6923)\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/3.png)
- Un dstribution stable, ou invariante, est
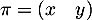 avec
avec 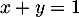 et
et
![\[\begin{array}{ll}\pi A= \pi
&\iff
\la\begin{array}{lclcl}
0,1x&+&0,4y&=&x\\
0,9x&+&0,6y&=&y\enar\right.\\[1.3em]
&\iff
\la\begin{array}{lclcl}
-0,9x&+&0,4y&=&0\\
0,9x&-&0,4y&=&0\enar\right.
\enar\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/6.png)
Ces deux équations sont équivalentes (l'opposée l'une de l'autre), et équivalente à
![\[x=\dfrac{0,4}{0,9}y=\dfrac49y\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/7.png)
Comme de plus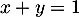 , on a donc
, on a donc
![\[x+y=\dfrac49y+y=\dfrac{13}9y=1\iff y=\dfrac9{13}\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/9.png)
On trouve alors aussi
![\[x+y=1 \iff x=1-y=\dfrac4{13}\]](/Generateur-Devoirs/Mex/markov/exetatstable_c/10.png)
La seule distribution invariante est donc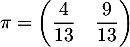
Tag:Chaines de Markov
Voir aussi:
Quelques devoirs
sur les graphes et chaînes de Markov. Evolution probabiliste et états stables. Traffic aérien entre 4 villes et équilibre de gaz entre deux réservoirs
