Répartition en deux opérateurs téléphoniques
Exercice corrigé - Maths expertes, terminale générale
Énoncé
Un opérateur téléphonique A souhaite prévoir l'évolution du nombre de ses abonnés dans une grande ville par rapport à son principal concurrent B à partir de 2013.
En 2013, les opérateurs A et B ont chacun 300 milliers d'abonnés.
Pour tout entier naturel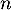 , on note
, on note 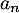 le nombre d'abonnés, en milliers, de l'opérateur A la n-ième année après 2013, et
le nombre d'abonnés, en milliers, de l'opérateur A la n-ième année après 2013, et 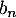 le nombre d'abonnés, en milliers, de l'opérateur B la n-ième année après 2013.
le nombre d'abonnés, en milliers, de l'opérateur B la n-ième année après 2013.
Ainsi,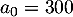 et
et 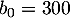 .
.
Des observations réalisées les années précédentes conduisent à modéliser la situation par la relation suivante :
pour tout entier naturel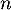 ,
,
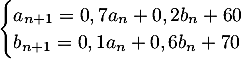 .
.
On considère les matrices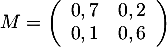 et
et
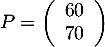 , et on note, pour tout entier naturel
, et on note, pour tout entier naturel 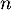 ,
,
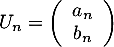 .
.
En 2013, les opérateurs A et B ont chacun 300 milliers d'abonnés.
Pour tout entier naturel
Ainsi,
Des observations réalisées les années précédentes conduisent à modéliser la situation par la relation suivante :
pour tout entier naturel
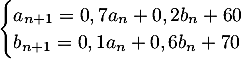 .
.
On considère les matrices
-
- Déterminer
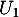 .
.
- Écrire matriciellement le système donnant
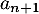 et
et 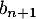
- Déterminer
- On note
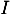 la matrice
la matrice
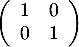 .
.
- Calculer
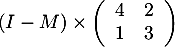 .
.
- En déduire que la matrice
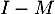 est inversible et préciser son inverse.
est inversible et préciser son inverse.
- Déterminer la matrice
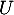 telle que
telle que 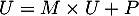 .
.
- Calculer
- Pour tout entier naturel, on pose
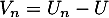 .
.
Justifier que, pour tout entier naturel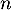 ,
, 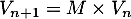 .
.
En déduire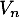 en fonction de
en fonction de 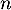 et de la matrice
et de la matrice 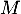 .
.
- On admet que, pour tout entier naturel
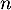 ,
,
![\[V_n = \lp\begin{array}{cc}
\dfrac{-100}{3}\times 0,8^n - \dfrac{140}{3} \times 0,5^n \\[1em]
\dfrac{-50}{3} \times 0,8^n + \dfrac{140}{3} \times 0,5^n
\enar\rp\]](/Generateur-Devoirs/Mex/markov/ex2/28.png)
- Pour tout entier naturel
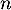 , exprimer
, exprimer 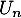 en fonction de
en fonction de 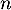 et en déduire la limite de la suite
et en déduire la limite de la suite 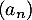 .
.
- Estimer le nombre d'abonnés de l'opérateur A à long terme.
- Pour tout entier naturel
Correction
Correction
(Bac S, Polynésie 7 juin 2013)-
-
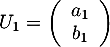
Or![$\begin{array}{ll}&\la\begin{array}{rcrcrcc}
a_1 &=& 0,7a_0 &+& 0,2b_0 &+& 60 \\
b_1 &=& 0,1a_0 &+& 0,6b_0 &+& 70\enar\right.\\[1.3em]
\iff &\la\begin{array}{rcrcrcc}
a_1 &=& 0,7 \times 300 &+& 0,2\times 300 &+& 60 \\
b_1 &=& 0,1\times 300 &+& 0,6\times 300 &+& 70
\enar\right.\enar$](/Generateur-Devoirs/Mex/markov/ex2_c/2.png)
Finalement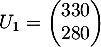
- Pour tout entier naturel
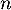 ,
, 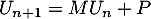
-
-
-
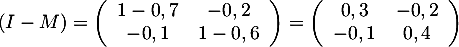 .
Puis on trouve
.
Puis on trouve
![\[\begin{array}{ll}
&(I-M) \times \lp\begin{array}{cc}4 & 2 \\ 1 & 3\enar\rp\\[1em]
=& \lp\begin{array}{cc}
4 \times 0,3 - 0,2 & 2 \times 0,3 - 3 \times 0,2 \\
-0,1 \times 4 + 0,4 & -0,1 \times 2 + 3 \times 0,4
\enar\rp\\[1.2em]
=& \lp\begin{array}{cc}1 & 0 \\ 0 & 1\enar\right) = I\enar\]](/Generateur-Devoirs/Mex/markov/ex2_c/7.png)
- On déduit du calcul précédent que
 est bien inversible, avec
est bien inversible, avec

-
![\[\begin{array}{ll}
&U = M \times U + P \\
\iff& U - M \times U = P \\
\iff& (I - M) \times U = P \\
\iff& U = (I-M)^{-1} P \enar\]](/Generateur-Devoirs/Mex/markov/ex2_c/10.png)
Finalement .
.
-
- Pour tout entier naturel
 ,
,
![\[\begin{array}{ll}
V_{n+1} &= U_{n+1} - U \\[.4em]
&= MU_n+P-(MU+P) \\[.em]
&= M(U_n-U)\\[.4em]
&= MV_n\enar\]](/Generateur-Devoirs/Mex/markov/ex2_c/13.png)
On en déduit que est une suite géométrique avec donc, pour tout entier
est une suite géométrique avec donc, pour tout entier 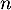 ,
,
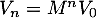
-
- Pour tout entier naturel
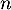 ,
,
![\[V_n = U_n-U \iff U_n = V_n+U
\iff U_n = \begin{pmatrix}
\dfrac{-100}{3}\times 0,8^n - \dfrac{140}{3} \times 0,5^n + 380 \\[1em]
\dfrac{-50}{3} \times 0,8^n + \dfrac{140}{3} \times 0,5^n + 270
\end{pmatrix} \]](/Generateur-Devoirs/Mex/markov/ex2_c/18.png)
On en déduit donc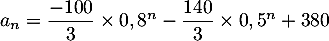
Comme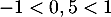 et
et 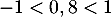 on a les limites
on a les limites
![\[\lim_{n\to+\infty}0,5^n=\lim_{n\to+\infty}0,8^n=0\]](/Generateur-Devoirs/Mex/markov/ex2_c/22.png)
et alors
![\[\lim_{n \rightarrow +\infty} a_n = 380\]](/Generateur-Devoirs/Mex/markov/ex2_c/23.png)
- Le nombre d'abonnés de l'opérateur A à long terme est donc de 380 000.
- Pour tout entier naturel
Tag:Chaines de Markov
Voir aussi:
Quelques devoirs
sur les graphes et chaînes de Markov. Evolution probabiliste et états stables. Traffic aérien entre 4 villes et équilibre de gaz entre deux réservoirs
