Part de marché
Exercice corrigé - Maths expertes, terminale générale
Énoncé
Dans un pays, deux opérateurs de téléphonie mobile AFR et BFM se partagent le marché.
En 2005, AFR en controlait 80% et BFM 20%.
On a ensuite observé, dans les années suivantes, que d'une année sur l'autre:
Pour tout naturel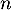 , on note respectivement
, on note respectivement 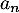 et
et 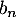 les part de marché de AFR et BFM l’année (2005 +
les part de marché de AFR et BFM l’année (2005 + 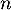 ).
Ainsi
).
Ainsi  et
et 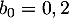 .
.
- 60% de la clientèle de AFR lui reste fidèle, tandis que 40% passe chez BFM.
- 70% de la clientèle de BFM lui reste fidèle, tandis que 30% passe chez AFR.
Pour tout naturel
- Traduire avec les données de l'énoncé le système donnant
 et
et  en fonction de
en fonction de  et
et 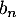 .
.
- On pose
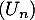 la suite matrices colonnes telle que
la suite matrices colonnes telle que 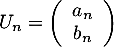 .
.
- Écrire le système d'équation de la première sous forme matricielle
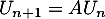 , en précisant la matrice
, en précisant la matrice  .
.
- En déduire
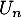 en fonction de
en fonction de  et de
et de  . À l'aide de la calculatrice donner
. À l'aide de la calculatrice donner  .
.
- Écrire le système d'équation de la première sous forme matricielle
-
- En se rappelant que
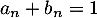 , déterminer les matrices
, déterminer les matrices 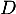 et
et 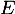 telles que :
telles que :
 où
où  est une matrice diagonale et
est une matrice diagonale et 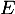 une matrice colonne.
une matrice colonne.
- Déterminer la matrice colonne
 telle que:
telle que: 
- On pose la suite de matrice
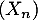 telle que:
telle que: 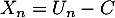 .
Montrer que:
.
Montrer que: 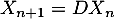 .
.
- En déduire alors
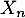 puis
puis 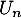 en fonction de
en fonction de  ,
,  et
et  .
.
- Montrer alors que
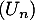 converge vers
converge vers  .
.
- En se rappelant que
Correction
Correction
- On a le système
![\[\la\begin{array}{rcrcr}
a_{n+1} &=& 0,6a_n &+& 0,3b_n\\
b_{n+1} &=& 0,4a_n &+& 0,7b_n\\
\enar\right.\]](/Generateur-Devoirs/Mex/markov/ex1_c/1.png)
-
- En posant la matrice
 , le système précédent se réécrit matriciellement
, le système précédent se réécrit matriciellement  .
.
- La suite
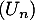 est une suite géométrique, et on a alors explicitement
est une suite géométrique, et on a alors explicitement 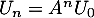 .
.
En particulier, on trouve avec l'aide d'une calculatrice,
![\[U_15=A^{15}U_0=\lp\begin{array}{c}0,4286\\0,5714\enar\rp\]](/Generateur-Devoirs/Mex/markov/ex1_c/6.png)
- En posant la matrice
-
- En utilisant la relation
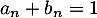 , le premier système se réécrit
, le premier système se réécrit
![\[\begin{array}{ll}&\la\begin{array}{rcrcr}
a_{n+1} &=& 0,6a_n &+& 0,3(1-a_n)\\
b_{n+1} &=& 0,4(1-b_n) &+& 0,7b_n\\
\enar\right.\\[1em]
&\iff
\la\begin{array}{rcrcr}
a_{n+1} &=& 0,3a_n &+& 0,3\\
b_{n+1} &=& 0,3b_n &+& 0,4\\
\enar\right.\enar\]](/Generateur-Devoirs/Mex/markov/ex1_c/8.png)
On pose cette les matrices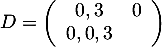 et
et  , et ce dernier système s'écrit matriciellement
, et ce dernier système s'écrit matriciellement
 .
.
-
![\[\begin{array}{ll}
&C = DC + E\\
\iff &C-DC=E\\
\iff &(I_2-D)C=E\enar\]](/Generateur-Devoirs/Mex/markov/ex1_c/12.png)
avec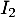 la matrice identité.
la matrice identité.
On a ici dont le déterminant vaut
dont le déterminant vaut  , ce qui montre que cette matrice est inversible et alors
, ce qui montre que cette matrice est inversible et alors
![\[(I_2-D)^{-1}=\dfrac1{0,49}\lp\begin{array}{cc}0,7&0\\0&0,7\enar\rp=\dfrac1{0,7}I_2\]](/Generateur-Devoirs/Mex/markov/ex1_c/16.png)
On trouve alors
![\[C=(I_2-D)^{-1}E=\dfrac1{0,7}I_2\lp\begin{array}{c}0,3\\0,4\enar\rp=\lp\begin{array}{c}\dfrac{0,3}{0,7}\\\dfrac{0,4}{0,7}\enar\rp\]](/Generateur-Devoirs/Mex/markov/ex1_c/17.png)
soit encore
![\[C=\dfrac17\lp\begin{array}{c}3\\4\enar\rp\]](/Generateur-Devoirs/Mex/markov/ex1_c/18.png)
- On a
![\[X_{n+1} = U_{n+1} - C
= DU_n+E - C\]](/Generateur-Devoirs/Mex/markov/ex1_c/19.png)
or , d'où
, d'où
![\[X_{n+1}DU_n+E -(DC+E) = D(U_n-C) = DX_n\]](/Generateur-Devoirs/Mex/markov/ex1_c/21.png)
- On en déduit que
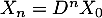 , avec la matrice
, avec la matrice
![\[D^n=\lp\begin{array}{cc}0,3^n&0\\0&0,3^n\enar\rp\]](/Generateur-Devoirs/Mex/markov/ex1_c/23.png)
et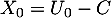 .
.
On revient ensuite à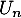 par la relation
par la relation
![\[X_n=U_n-C \iff U_n=X_n+C=D^nX_0+C\]](/Generateur-Devoirs/Mex/markov/ex1_c/26.png)
- Comme
 , on a
, on a 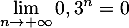 et donc on trouve que
et donc on trouve que
![\[\lim_{n\to+\infty}D^n=\lp\begin{array}{cc}0&0\\0&0\enar\rp\]](/Generateur-Devoirs/Mex/markov/ex1_c/29.png)
et donc que
![\[\lim_{n\to+\infty}X_n=C\]](/Generateur-Devoirs/Mex/markov/ex1_c/30.png)
- En utilisant la relation
Tag:Chaines de Markov
Voir aussi:
Quelques devoirs
sur les graphes et chaînes de Markov. Evolution probabiliste et états stables. Traffic aérien entre 4 villes et équilibre de gaz entre deux réservoirs
