Traffic aérien entre 4 villes
Exercice corrigé - Maths expertes, terminale générale
Énoncé
On considère quatre villes 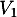 ,
, 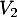 ,
, 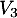 et
et 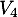 et le traffic aérien qui permet de relier ces quatre villes: il existe seulement des vols directs
et le traffic aérien qui permet de relier ces quatre villes: il existe seulement des vols directs
- de
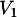 vers
vers 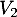 et de
et de 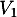 vers
vers 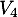 ,
,
- de
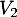 vers
vers 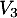 ,
,
- de
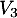 vers
vers 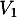 et de
et de 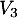 vers
vers 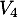 ,
,
- de
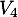 vers
vers 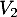
- Recopier et compléter le graphe suivant.
{$V_2$}
\rput(3,0){$\bullet$}\rput[l](3.2,0){$V_4$}
\rput(0,-3){$\bullet$}\rput(0,-3.3){$V_3$}
\psarc{<-}(0,0){3}{5}{85}
\psarc{->}(0,0){3}{95}{175}
\end{pspicture}\]](/Generateur-Devoirs/Mex/markov/extraffic/17.png)
- Écrire la matrice
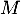 associée à ce graphe, en prenant les villes dans leur ordre de numération.
associée à ce graphe, en prenant les villes dans leur ordre de numération.
- Donner les matrices
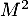 ,
, 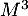 et
et 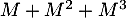 .
.
- Combien de vols comportant au plus deux escales permettent de relier
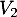 à
à 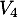 ?
?
- Existe t-il au moins un vol de chaque ville
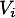 vers chaque ville
vers chaque ville 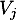 comportant au plus deux escales ? Pourquoi ?
comportant au plus deux escales ? Pourquoi ?
Correction
Correction
-
{$V_2$}
\rput(3,0){$\bullet$}\rput[l](3.2,0){$V_4$}
\rput(0,-3){$\bullet$}\rput(0,-3.3){$V_3$}
\psarc{<-}(0,0){3}{5}{85}
\psarc{->}(0,0){3}{95}{175}
%
\psarc{->}(0,0){3}{185}{265}
\psarc{->}(0,0){3}{275}{355}
\psarc{->}(-3,0){4.3}{318}{42}
\psarc{->}(0,-3.2){4.3}{50}{131}
\end{pspicture}\]](/Generateur-Devoirs/Mex/markov/extraffic_c/1.png)
- La matrice associée à ce graphe est
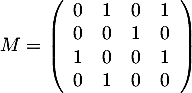 .
.
On a ensuite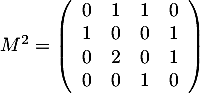 .
et
.
et
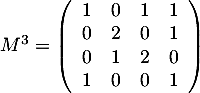 .
et donc
.
et donc
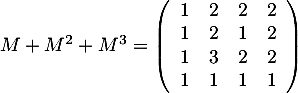 .
.
- La matrice d'adjacence
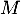 contient les vols directs entre les villes,
contient les vols directs entre les villes, 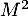 contient les nombres de vols avec exactement une escale, et
contient les nombres de vols avec exactement une escale, et 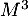 les nombres de vols avec exactement 2 escales.
les nombres de vols avec exactement 2 escales.
On trouve ainsi, dans la matrice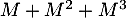 qu'il y a 2 vols avec au plus deux escales qui permettent de relier
qu'il y a 2 vols avec au plus deux escales qui permettent de relier 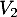 à
à 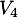 .
.
- Comme la matrice
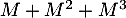 ne contient aucun zéro, toute ville
ne contient aucun zéro, toute ville 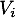 peut être reliée à chaque ville
peut être reliée à chaque ville 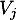 avec au plus deux escales.
avec au plus deux escales.
Tag:Chaines de Markov
Voir aussi:
Quelques devoirs
sur les graphes et chaînes de Markov. Evolution probabiliste et états stables. Traffic aérien entre 4 villes et équilibre de gaz entre deux réservoirs
