Matrice d'ordre 2 et système d'équations

Exercice corrigé - Maths expertes, terminale générale

Énoncé

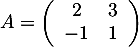  1. Soit $A=\lp\begin{array}{cc}2&3\\-1&1\enar\rp$.
    Montrer que la matrice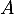 $A$ est inversible est donner son inverse.
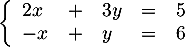
  2. Soit le système $\la\begin{array}{lclcl}2x&+&3y&=&5\\ -x&+&y&=&6\enar\right.$
    Écrire ce système sous forme matriciel, et résoudre alors matriciellement ce système.



Correction

Correction

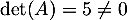  1. On a $\det(A)=5\not=0$ et cette matrice est donc bien inversible, avec
    \[A^{-1}=\dfrac15\lp\begin{array}{cc}1&-3\\1&2\enar\rp\]


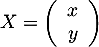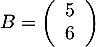  2. En posant $X=\lp\begin{array}{c}x\\y\enar\rp$ et $B=\lp\begin{array}{c}5\\6\enar\rp$, le système s'écrit matriciellement sous la forme 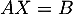$AX=B$, et comme on sait que 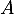$A$ est inversible et qu'on connaît son inverse,
    \[AX=B\iff X=A^{-1}B\]

    Soit
    \[\lp\begin{array}{c}x\\y\enar\rp=\dfrac15\lp\begin{array}{cc}1&-3\\1&2\enar\rp\lp\begin{array}{c}5\\6\enar\rp=\dfrac15\lp\begin{array}{c}-13\\17\enar\rp\]

    soit la solution
    \[x=-\dfrac{13}5 \ \text{ et } \ y=\dfrac{17}5\]



Tag:matrices

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs


LongPage: h2: 3 - h3: 0