Diagonalisation et suite géométrique
Exercice corrigé - Maths expertes, terminale générale
Énoncé
On considère la matrice 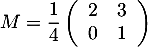 .
.
On cherche à exprimer la matrice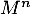 explicitement en fonction de
explicitement en fonction de 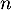 .
.
On considère la matrice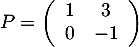 .
.
On cherche à exprimer la matrice
On considère la matrice
- Montrer que
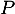 est sa propre inverse.
est sa propre inverse.
- Montrer que la matrice
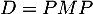 est une matrice diagonale.
est une matrice diagonale.
En déduire que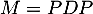 .
.
- Montrer que, pour tout entier
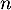 ,
, 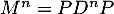 .
.
- En déduire l'expression de
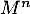 en fonction de
en fonction de 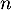 .
.
- On définit la suite
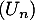 par
par 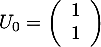 , puis, pour tout entier
, puis, pour tout entier 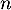 ,
, 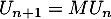 .
.
- Calculer
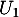 et
et 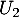 .
.
- Exprimer
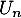 en fonction de
en fonction de 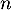 .
.
- Calculer
Correction
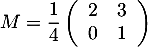 et
et 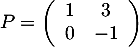 .
.
Correction
On considère les matrices-
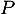 est sa propre inverse si
est sa propre inverse si 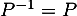 , c'est-à-dire si
, c'est-à-dire si
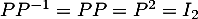 .
.
On calcule donc
![\[P^2=\lp\begin{array}{cc}1&3\\0&-1\enar\rp\lp\begin{array}{cc}1&3\\0&-1\enar\rp
=\lp\begin{array}{cc}1&0\\0&1\enar\right)
\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/6.png)
ce qui montre bien que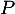 est inversible et qu'elle est sa propre inverse.
est inversible et qu'elle est sa propre inverse.
- On calcule ce produit matriciel (dans l'ordre souhaité, car le produit est associatif, mais attention, sans permuter deux matrices car le produit n'est par contre pas commutatif)
![\[\begin{array}{ll}D=PMP\\
&=\lp\begin{array}{cc}1&3\\0&-1\enar\rp\dfrac14\lp\begin{array}{cc}2&3\\0&1\enar\rp\lp\begin{array}{cc}1&3\\0&-1\enar\rp\\[1.2em]
&=\dfrac14\lp\begin{array}{cc}2&6\\0&-1\enar\rp\lp\begin{array}{cc}1&3\\0&-1\enar\rp\\[1.2em]
&=\dfrac14\lp\begin{array}{cc}2&0\\0&1\enar\right)
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/8.png)
est bien une matrice diagonale.
On en déduit, multipliant à gauche par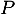 et avec
et avec 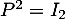 , que
, que
![\[D=PMP\iff PD=P^2MP=MP\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/11.png)
puis en multipliant à droite par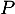 ,
,
![\[PDP=MP^2=M\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/13.png)
d'où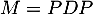 .
.
- On a donc
![\[M^n=(PDP)^n
=(PDP)(PDP)\dots(PDP)\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/15.png)
soit, comme le produit matriciel est associatif,
![\[\begin{array}{ll}M^n&=PD\underbrace{PP}_{=I_2}D\underbrace{PP}_{=I_2}D\dots DP\\
&=PDD\dots DP\\
&=PD^nP
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/16.png)
- On a facilement
![\[D^n=\dfrac1{4^n}\lp\begin{array}{cc}2^n&0\\0&1^n\enar\rp=\dfrac1{4^n}\lp\begin{array}{cc}2^n&0\\0&1\enar\rp\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/17.png)
et donc
![\[\begin{array}{ll}M^n=PD^nP
&=\lp\begin{array}{cc}1&3\\0&-1\enar\rp\dfrac1{4^n}\lp\begin{array}{cc}2^n&0\\0&1\enar\rp\lp\begin{array}{cc}1&3\\0&-1\enar\rp\\[1.2em]
&=\dfrac1{4^n}\lp\begin{array}{cc}2^n&3\\0&-1\enar\rp\lp\begin{array}{cc}1&3\\0&-1\enar\rp\\[1.2em]
&=\dfrac1{4^n}\lp\begin{array}{cc}2^n&3\tm\lp2^n-1\rp\\0&1\enar\rp
\end{array}
\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/18.png)
- On définit la suite
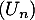 par
par 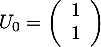 , puis, pour tout entier
, puis, pour tout entier 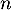 ,
, 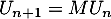 .
.
-
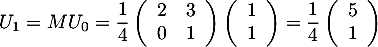
et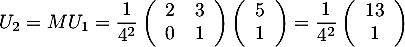
-
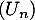 est une suite géométrique, donc pour tout entier
est une suite géométrique, donc pour tout entier 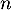 ,
,
![\[U_n=M^nU_0\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/27.png)
soit, d'après la question précédente,
![\[\begin{array}{ll}U_n&=\dfrac1{4^n}\lp\begin{array}{cc}2^n&3\tm\lp2^n-1\rp\\0&1\enar\rp\lp\begin{array}{c}1\\1\enar\rp\\[1.2em]
&=\dfrac1{4^n}\lp\begin{array}{c}2^n+3\lp2^n-1\rp\\1\enar\rp
\enar\]](/Generateur-Devoirs/Mex/Matrices/exdiagogeom_c/28.png)
(résultat qu'on peut vérifier pour les cas ,
, 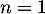 et
et  )
)
-
Tag:matrices
Voir aussi:
Quelques devoirs
sur les matrices et calcul matriciel, produit, puissance d'une matrice, définition de l'inverse d'une matrice
sur la factorisation et racines d'un polynôme complexe et matrices et calcul matriciel, diagonalisation et limites de suites
sur binôme de Newton et les racines de l'unité. Calcul de la puissance n-ième d'une matrice
sur les matrices, calcul matriciel et les nombres complexes: géométrie, formes algébriques et exponentielles.
