Préparer l'épreuve de spécialité du bac: intégration
Terminale générale, spécialité mathématiques
Quelques exercices sur les intégrales, primitives, l'intégration et un peu de suite d'intégrales, et leur correction, pour s'entraîner et préparer l'épreuve écrite de spécialité de mathématiques au baccalauréat général. Des calculs d'intégrales, intégration par parties et autres suites s'intégrales au programme...
Exercice 1: Calculs d'intégrales
Calculer les intégrales:
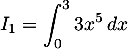 ;
;
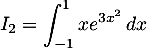 ;
;
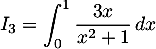 ;
;
À l'aide d'une intégration par parties, calculer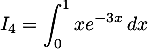
À l'aide d'une intégration par parties, calculer
Exercice 2: Calcul d'une aire entre deux courbes de logarithmes
Les courbes C et C' données ci-dessous représentent respectivement, dans un repère orthonormal 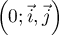 , les fonctions
, les fonctions 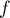 et
et 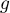 définies sur l'intervalle
définies sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/4.png) par
par 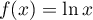 et
et 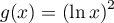 .
.
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
Bac juin 2008
Cacher la correction
![\[\psset{xunit=3cm,yunit=1.5cm}
\begin{pspicture*}(-1,-3.2)(4,3.2)
\newcommand{\f}[1]{x ln}
\newcommand{\g}[1]{x ln 2 exp}
\pscustom{
\psplot{1}{2.718}{\f{x}} \gsave
\psplot{2.718}{1}{\g{x}}
\fill[fillstyle=solid,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline(-.2,0)(4,0)
\psline(0,-3)(0,3)
\multido{\i=1+1}{4}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\multido{\i=-3+1}{7}{\psline(-.1,\i)(.1,\i)\rput[r](-.1,\i){\i}}
\psplot{.05}{4}{\f{x}}
\psplot{.1}{4}{\g{x}}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/7.png)
- On cherche à déterminer l'aire A (en unités d'aire) de la partie grisée.
On note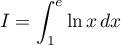 et
et 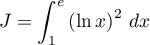 .
.
- Vérifier que la fonction
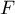 définie sur l'intervalle
définie sur l'intervalle ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/11.png) par
par
 est une primitive de la fonction logarithme népérien.
En déduire
est une primitive de la fonction logarithme népérien.
En déduire 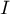 .
.
- Démontrer à l'aide d'une intégration par partie que
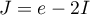 .
.
- Donner la valeur de A.
- Vérifier que la fonction
- Pour
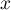 appartenant à l'intervalle
appartenant à l'intervalle ![$[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP/16.png) , on note
, on note 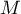 le point de la courbe C d'abscisse
le point de la courbe C d'abscisse 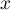 et
et  le point de la courbe C' de même abscisse.
le point de la courbe C' de même abscisse.
Pour quelle valeur de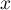 la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
la distance MN est-elle maxiale ?
Calculer la valeur maximale de MN.
Correction exercice 2
Bac juin 2008
-
- On dérive:
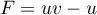 avec
avec 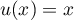 donc
donc  et
et 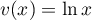 donc
donc  ,
,
et alors,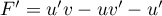 ,
,
soit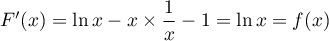
ce qui montre que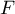 est bien une primtive de
est bien une primtive de 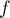 .
.
On en déduit
![\[\begin{array}{ll}I&=\dsp\int_1^e\ln x\,dx
=\Bigl[\,F(x)\,\Bigr]_1^e
=F(e)-F(1)\\[1em]
&=\left( e\ln e-e\rp-\left( 1\ln 1-1\rp
=1\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/10.png)
- On pose
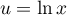 donc
donc 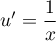 et
et 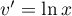 donc
donc 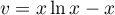 et et alors, en intégrant par parties,
et et alors, en intégrant par parties,
![\[\begin{array}{ll}J&=\Bigl[\ln x\left( x\ln x-x\rp\Bigr]_1^e
-\dsp\int_1^e\dfrac1x\left( x\ln x-x\rp\\[1em]
&=0-\dsp\int_1^e\lp\ln x-1\rp\,dx\\[1em]
&=-\dsp\int_1^e\ln x\,dx+\int_1^e1dx\\[1em]
&=-I+e-1=e-2I\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/15.png)
car .
.
- On en déduit la valeur de A:
![\[\begin{array}{ll}A&=\dsp\int_1^e\left( f(x)-g(x)\rp\,dx\\[1em]
&=\dsp\int_1^ef(x)\,dx-\int_1^eg(x)\,dx\\[1em]
&=I-J
=1-\left( e-2I\rp\\
&=1-\left( e-2\rp=3-e\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/17.png)
- On dérive:
- Pour
![$x\in[1;e]$](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/18.png) , on a
, on a
![\[\begin{array}{ll}MN&=d(x)=f(x)-g(x)\\[.5em]&=\ln x-\lp\ln x\rp^2\enar\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/19.png)
Pour trouver le maximum de cette fonction, il suffit de connaître ses variations.
On a
![\[d'(x)=\dfrac1x-2\dfrac1x\ln x=\dfrac1x\lp1-2\ln x\rp\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/20.png)
avec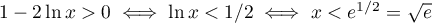 et donc
et donc
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$1$ && $\sqrt{e}$ && $e$\\\hline
$1/x$ && $+$ &$|$&$+$&\\\hline
$1-2\ln x$ && $+$ &\zb&$-$&\\\hline
$d'(x)$ && $+$ &\zb&$-$&\\\hline
&&&$d\lp\sqrt{e}\rp$&&\\
$d$&&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/22.png)
La distance est donc maximale en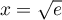 et cette distance maximale est
et cette distance maximale est
![\[d\lp\sqrt{e}\rp=\ln\sqrt{e}-\lp\ln\sqrt{e}\rp^2
=\dfrac12-\lp\dfrac12\rp^2=\dfrac14\]](/Generateur-Devoirs/TS/ChapIntegration/exLogCarreIPP_c/24.png)
Cacher la correction
Exercice 3: Suite d'intégrales avec exponentielles
Bac S, 19 juin 2014, 5 points
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par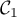 la courbe représentative de la fonction
la courbe représentative de la fonction 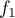 définie sur
définie sur 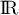 par:
par:
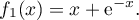
Partie B
L'objet de cette partie est d'étudier la suite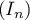 définie sur
définie sur 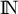 par:
par:
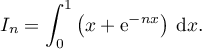
Partie A
Partie B
Cacher la correction
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par
- Justifier que
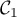 passe par le point A de coordonnées
passe par le point A de coordonnées 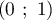 .
.
- Déterminer le tableau de variation de la fonction
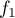 . On
précisera les limites de
. On
précisera les limites de 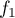 en
en 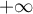 et en
et en 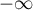 .
.
Partie B
L'objet de cette partie est d'étudier la suite
- Dans le plan muni d'un repère orthonormé
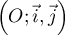 ,
pour tout entier
naturel
,
pour tout entier
naturel 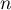 , on note
, on note 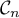 la courbe représentative de la
fonction
la courbe représentative de la
fonction 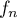 définie sur
définie sur 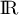 par
par
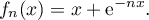
Sur le graphique ci-dessous on a tracé la courbe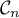 pour plusieurs valeurs de l'entier
pour plusieurs valeurs de l'entier 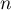 et la droite
et la droite 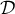 d'équation
d'équation 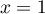 .
.
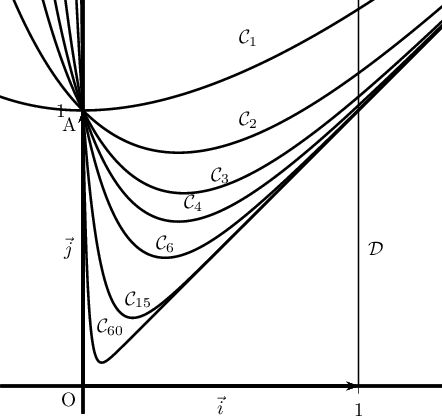
- Interpréter géométriquement l'intégrale
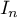 .
.
- En utilisant cette interprétation, formuler une conjecture sur
le sens de variation de la suite
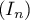 et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
- Interpréter géométriquement l'intégrale
- Démontrer que pour tout entier naturel
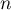 supérieur ou égal à 1,
supérieur ou égal à 1,
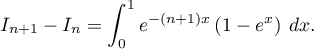
En déduire le signe de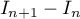 puis démontrer que la suite
puis démontrer que la suite
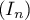 est convergente.
est convergente.
- Déterminer l'expression de
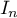 en fonction de
en fonction de 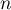 et
déterminer la limite de la suite
et
déterminer la limite de la suite 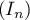 .
.
Correction exercice 3
Partie A
- On a
 et donc
et donc  .
.
- Comme
 et
et  sont définies et dérivables
sur
sont définies et dérivables
sur  ,
,  est aussi définie et dérivable sur
est aussi définie et dérivable sur  , comme somme
et composéee de fonctions définies et dérivables sur
, comme somme
et composéee de fonctions définies et dérivables sur  ,
avec,
pout tout
,
avec,
pout tout  ,
,  .
.
De plus, ,
car la fonction exponentielle est strictement croissante sur
,
car la fonction exponentielle est strictement croissante sur  ,
et ainsi,
,
et ainsi,  .
.
En ,
,  et
et
 , et donc,
par somme des limites,
, et donc,
par somme des limites,  .
.
En ,
,
 , avec
, avec
 et
et
 (croissance comparée en l'infini de
l'exponentielle et des polynômes).
(croissance comparée en l'infini de
l'exponentielle et des polynômes).
Ainsi, , et alors, par
produit des limites,
, et alors, par
produit des limites,
 .
.

Partie B
-
-
 est l'aire sous la courbe
est l'aire sous la courbe  :
l'aire du domaine compris entre les droites verticales
d'équation
:
l'aire du domaine compris entre les droites verticales
d'équation  et
et  , et entre l'axe des abscisses et la
courbe
, et entre l'axe des abscisses et la
courbe  .
.
- Il semblerait que la courbe
 soit en
dessous de la courbe
soit en
dessous de la courbe  .
On peut donc conjecturer que la suite
.
On peut donc conjecturer que la suite  est décroissante.
est décroissante.
Il semblerait de plus que lorsque devient grand, la courbe
devient grand, la courbe
 se rapproche de la diagonale du carré de côté
se rapproche de la diagonale du carré de côté
 .
On peut ainsi conjecturer que la suite
.
On peut ainsi conjecturer que la suite  est
convergente, de limite
est
convergente, de limite  .
.
-
- Pour tout entier
 ,
,

car .
.
De plus, pour tout ,
,
 ,
et
,
et  , car la fonction exponentielle est strictement
croissante sur
, car la fonction exponentielle est strictement
croissante sur  , et donc,
, et donc,  .
.
On en déduit que pour tout ,
,
 ,
et donc que
,
et donc que

Ainsi, la suite est décroissante.
est décroissante.
Comme pour tout et pour tout entier
et pour tout entier  ,
,
 , et donc,
, et donc,  ,
on a
,
on a  .
.
Ainsi, est une suite décroissante et minorée par 0:
est une suite décroissante et minorée par 0:
 est donc convergente.
est donc convergente.
- Pour tout entier
 ,
,

Comme et
et  ,
on a donc,
,
on a donc,
 ,
ce qui démontre la conjecture émise au début de cette partie.
,
ce qui démontre la conjecture émise au début de cette partie.
Cacher la correction
Exercice 4: Encadrement et limite d'une suite d'intégrales
On considère la suite 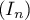 définie pour tout entier naturel
définie pour tout entier naturel 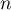 par
l'expression
par
l'expression
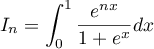
Cacher la correction
- Calculer l'intégrale
 .
.
- Calculer
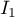 .
.
- Déterminer le sens de variation de la suite
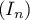 .
.
- Montrer que pour tout réel
![$x\in[0;1]](/Generateur-Devoirs/TS/ChapSuitesInt/exOral01/7.png) ,
,
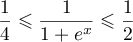 .
.
- En déduire un encadrement de
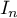 puis la limite de la suite
puis la limite de la suite 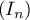 .
.
Correction exercice 4
-
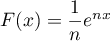 est une primitive de
est une primitive de 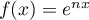 ,
et ainsi
,
et ainsi

-
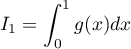 , avec
, avec 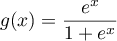 .
On reconnaît une expression à intégrer de la forme
.
On reconnaît une expression à intégrer de la forme 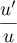 avec
avec
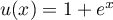 .
.
Ainsi,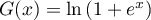 est une primitive de
est une primitive de  , et on a donc,
, et on a donc,
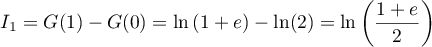
- Pour tout entier
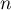 , on a, par linéarité de l'intégrale,
, on a, par linéarité de l'intégrale,
![\begin{array}{ll}
I_{n+1}-I_n
&\dsp=\int_0^1\dfrac{e^{(n+1)x}}{1+e^x}dx-\int_0^1\dfrac{e^{nx}}{1+e^x}dx\\[.5cm]
&\dsp=\int_0^1\lp\dfrac{e^{(n+1)x}}{1+e^x}-\dfrac{e^{nx}}{1+e^x}\right) dx\\[.5cm]
&\dsp=\int_0^1\dfrac{e^{(n+1)x}-e^{nx}}{1+e^x}dx\\[.5cm]
&\dsp=\int_0^1\dfrac{e^{nx}\left( e^x-1\rp}{1+e^x}dx\\[.5cm]
\enar](/Generateur-Devoirs/TS/ChapSuitesInt/exOral01_c/12.png)
Or, pour tout![$x\in[0;1]](/Generateur-Devoirs/TS/ChapSuitesInt/exOral01_c/13.png) ,
, 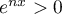 , et
, et 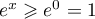 , car
la fonction exponentielle est croissante, d'où
, car
la fonction exponentielle est croissante, d'où 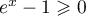 ,
et
,
et  .
.
Ainsi, pour tout![$x\in[0;1]](/Generateur-Devoirs/TS/ChapSuitesInt/exOral01_c/18.png) ,
, 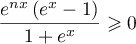 ,
et donc, par positivité de l'intégrale,
,
et donc, par positivité de l'intégrale,
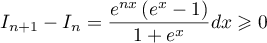
ce qui montre que la suite est croissante.
est croissante.
- La fonction exponentielle étant croissante sur
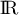 , on a
, on a
![x\in[0;1]\iff 0\leqslant x\leqslant 1 \iff e^0=1\leqslant
e^x\leqslant e^1=e\iff 2\leqslant 1+e^x\leqslant 1+e\leqslant 4](/Generateur-Devoirs/TS/ChapSuitesInt/exOral01_c/23.png)
car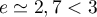 .
.
Ainsi, en prenant l'inverse (et en inversant donc l'ordre), on a bien, pour tout![$x\in[0;1]](/Generateur-Devoirs/TS/ChapSuitesInt/exOral01_c/25.png) ,
,
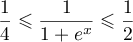 .
.
- Comme l'intégrale conserve l'ordre, on déduit de l'encadrement
précédent que
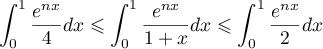
soit donc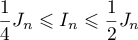 ,
et, grçace à la première question:
,
et, grçace à la première question:
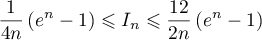
Comme, par croissances comparées,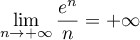 ,
on a donc
,
on a donc 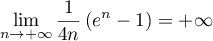 ,
et ainsi, d'après le corollaire du théorème des gendarmes,
,
et ainsi, d'après le corollaire du théorème des gendarmes,
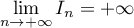 .
.
Cacher la correction
Quelques autres devoirs
intégration, Calculs d'intégrales - Suite d'intégrales (Bac S, 19 juin 2014) - Dimensionnement d'un récupérateur d'eau (Bac S - Amérique du nord, 1er juin 2016)
intégration, Calculs d'intégrales - Aire sous une courbe (Bac S - métropole, 11 septembre 2014) - Aire entre deux courbes (Bac S, juin 2008)
sur les intégrales: calcul d'intégrales, suite d'intégrales, et un calcul de volume
sur les intégrales: calcul d'intégrales, suite d'intégrales
Quelques exercices corrigés
Exercices corrigés
Bac 2014 (Antilles-Guyane) - Étude de fonctions, limites, TVI, tangente, intégrale
Exercices corrigés
Bac 2024 (19 juin): Logarithme, variation, limites et TVI, convexité et intégrale
Exercices corrigés
Bac 2013 - Fonction avec log, dérivée, limites, TVI, algorithme, intégrale
Exercices corrigés
Calculs d'intégrales
Exercices corrigés
Calculs d'intégrales (bis)
Voir aussi:
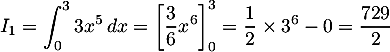
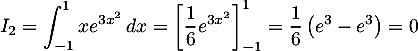
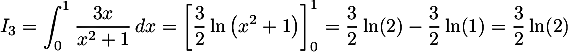
![\[\begin{array}{ll}I_4&=\dsp\int_0^1xe^{-3x}\,dx\\[1em]
&=\left[ -\dfrac13xe^{-3x}\rb_0^1-\dsp\int_0^1-\dfrac13e^{-3x}\,dx\\[1em]
&=-\dfrac13e^{-3}-\lb\dfrac19e^{-3x}\rb_0^1\\[1em]
&=-\dfrac13e^{-3}-\lp\dfrac19e^{-3}-\dfrac19e^0\rp\\[1em]
&=-\dfrac49e^{-3}+\dfrac19
\enar\]](/Generateur-Devoirs/TS/ChapIntegration/ex0b_c/8.png)