Oral du bac: suite, logarithme et exponentielle
Terminale générale, spécialité mathématiques
- L'utilisation d'une calculatrice est autorisée.
- La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.
- Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.
Exercice 1: Suite définie explicitement - Etude de fonction
Soit la fonction 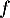 définie sur
définie sur 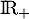 par l'expression
par l'expression
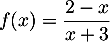 .
.
On considère la suite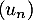 définie pour tout entier naturel
définie pour tout entier naturel 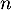 par
la relation
par
la relation 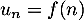 .
.
Cacher la correction
On considère la suite
- Calculer
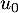 ,
, 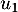 et
et 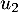 .
La suite
.
La suite 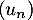 peut-elle être arithmétique ? géométrique ?
peut-elle être arithmétique ? géométrique ?
- Dresser la tableau de variation de la fonction
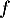 .
.
- En déduire le sens de variation de la suite
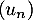 .
.
Correction exercice 1
-
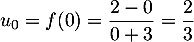 ,
,
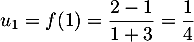 et
et
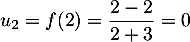 .
.
On a alors: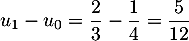 et
et
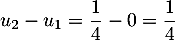 .
.
La suite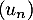 n'est donc pas arithmétique.
n'est donc pas arithmétique.
De même,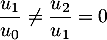 , et donc la suite
, et donc la suite 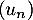 n'est pas non plus géometrique.
n'est pas non plus géometrique.
- Pour tout
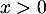 ,
,
![\[
f'(x)=\dfrac{-1\tm(x+3)-(2-x)\tm1}{(x+3)^2}
=\dfrac{-5}{(x+3)^2}
\]](/Generateur-Devoirs/TS/ChapSuites/exOral00_c/10.png)
et donc,
![\[\begin{tabular}{|c|cccc|}\hline
$x$ & $0$ \hspace{1cm} && \hspace{1cm} & $+\infty$\\\hline
$-5$ && $-$ && \\\hline
$(x+3)^2$ && $+$ && \\\hline
$f'(x)$ && $-$ && \\\hline
&&&&\\
$f$ && \psline{->}(-1,0.4)(1.4,-0.4) && \\
&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/exOral00_c/11.png)
- On en déduite que la suite
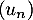 est décroissante.
est décroissante.
Cacher la correction
Exercice 2: Logarithme et exponentielles - Limites - Equation avec log et exp
Soit 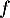 la fonction définie par l'expression
la fonction définie par l'expression  .
.
On note sa courbe dans un repère du plan.
sa courbe dans un repère du plan.
Cacher la correction
On note
- Quel est l'ensemble de définition de
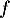 ?
?
- Etudier la limite de
 en
en 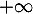 .
.
- Montrer que, pour tout réel
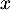 ,
,  .
.
- Résoudre l'équation
 en
en 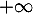 .
.
Correction exercice 2
- Le logarithme est défini sur
![$\R_+^*=]0;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exOral02_c/1.png) .
.
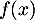 est ainsi défini pour les valeurs réelles de
est ainsi défini pour les valeurs réelles de  telles que
telles que
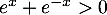 .
.
Or pour tout réel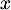 ,
, 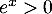 et
et  , donc
, donc 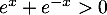 .
.
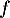 est ainsi définie sur
est ainsi définie sur 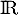 .
.
-
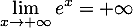 et
et
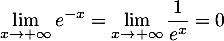 .
.
Ainsi, par somme des limites, ,
et, comme
,
et, comme 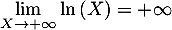 ,
par composition des limites,
,
par composition des limites,
 .
.
- Pour tout réel
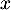 ,
,
![\[f(x)=\ln\left( e^x+e^{-x}\rp=\ln\left( e^x\left( 1+e^{-2x}\rp\rp=\ln\left( e^x\rp+\ln\left( 1+e^{-2x}\rp=x+\ln\left( 1+e^{-2x}\rp\]](/Generateur-Devoirs/TS/ChapLogarithme/exOral02_c/17.png)
-
![\[\begin{array}{ll}
f(x)=x+2&\iff x+\ln\lp1+e^{-2x}\rp=x+2\\[.5em]
&\iff\ln\lp1+e^{-2x}\rp=2\\[.5em]
&\iff 1+e^{-2x}=e^2\\[.5em]
&\iff e^{-2x}=e^2-1\\[.5em]
&\iff -2x=\ln\left( e^2-1\rp\\[.5em]
&\iff x=-\dfrac12\ln\left( e^2-1\rp\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exOral02_c/18.png)
Cacher la correction
Quelques autres devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
Quelques exercices corrigés
Exercices corrigés
Limites de 2 suites
Exercices corrigés
Limites de 4 suites
Exercices corrigés
Une petite récurrence
Exercices corrigés
Une petite récurrence
Exercices corrigés
Suite auxiliaire géométrique
Voir aussi: