Vérification d'une solution, étude de fonction, convexité
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction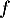 
définie sur 
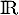par l'expression
.
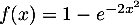Correction
définie sur par l'expression
.
- Montrer que
est solution de l'équation différentielle
.
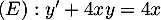- Déterminer les limites de
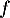en 
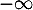et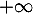 
, et les éventuelles asymptotes à la courbe de 
.
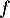- Étudier le sens de variation de
.
- Étudier la convexité de
.
Correction
Tags:Équations différentiellesExponentielleConvexité
Autres sujets au hasard:
Voir aussi:
Quelques devoirs
sur les équations différentielles: désintégration de noyaux radioactifs - Température de refroidissement d'un objet (Bac S, Antilles-Guyane, 23 juin 2009) - Équaton différentielle avec changement de fonction (Bac S, métropole, 22 juin 2010) - Équaton différentielle non linéaire, avec un carré
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité - Probabilités & loi binomiale - Suite récurrente
sur la résolution d'&quations différentielles