Devoir de maths corrigé, Equations différentielles
Terminale générale, spécialité mathématiques
Devoir de mathématiques, et corrigé, posé en spé maths, terminale générale, année scolaire 2022/2023
Exercice 1: Nombre de noyaux radioactifs
Nombre de noyaux radioactifs
On note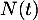 le nombre de noyaux radioactifs d'un corps à l'instant
le nombre de noyaux radioactifs d'un corps à l'instant 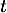 , où
, où 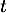 est exprimé en jours.
est exprimé en jours.
On admet que la fonction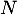 est solution de l’équation différentielle
est solution de l’équation différentielle
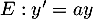 , où
, où 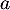 est une constante réelle.
est une constante réelle.
Cacher la correction
On note
On admet que la fonction
- Déterminer la fonction
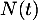 solution de l'équation différentielle
solution de l'équation différentielle 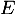 , sachant que
, sachant que 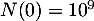 .
.
- Au bout de 18 jours, le nombre de noyaux radioactifs a diminué de moitié.
En déduire la valeur exacte de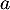 .
.
- Au bout de combien de jours le le nombre de noyaux radioactifs deviendra-t-il inférieur à 100 ?
Correction exercice 1
-
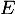 est une équation sans second membre
est une équation sans second membre 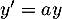 dont la solution est directement
dont la solution est directement 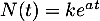 ,
, 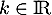 .
.
De plus, on a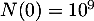 d'une part, et d'autre part,
d'une part, et d'autre part, 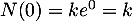 .
.
On en déduit que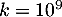 , et donc que la solution de
, et donc que la solution de  recherchée est
recherchée est 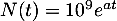 .
.
- Pour
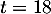 , on a
, on a
![\[N(18)=\dfrac{N(0)}2=\dfrac{10^9}2=10^9e^{18a}\]](/Generateur-Devoirs/TS/ChapEqDiff/radio_c/11.png)
On en déduit que
![\[e^{18a}=\dfrac12\iff a=-\dfrac1{18}\ln(2)\]](/Generateur-Devoirs/TS/ChapEqDiff/radio_c/12.png)
- On cherche
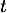 tel que
tel que
![\[\begin{array}{ll}N(t)<100 &\iff 10^9e^{at}<100\\
&\iff e^{at}<\dfrac{100}{10^9}=10^{-7}\enar\]](/Generateur-Devoirs/TS/ChapEqDiff/radio_c/14.png)
puis, en appliquant la fonction ln qui est strictement croissante,
![\[at<\ln(10^{-7})=-7\ln(10)\]](/Generateur-Devoirs/TS/ChapEqDiff/radio_c/15.png)
et enfin, en divisant par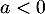 , on trouve
, on trouve
![\[t>-\dfrac7a\ln(10)=7\tm18\dfrac{\ln(10)}{\ln(2)}\simeq418\]](/Generateur-Devoirs/TS/ChapEqDiff/radio_c/17.png)
soit au cours du 418ème jour.
Cacher la correction
Exercice 2: Equation différentielle, exponentielle (Bac 2009, Antilles-Guyane)
La température de refroidissement d'un objet fabriqué industriellement
est une fonction  du temps
du temps 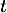 .
Cette fonction
.
Cette fonction 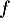 est définie sur l'ensemble des nombres réels positifs et vérifie
l'équation différentielle:
est définie sur l'ensemble des nombres réels positifs et vérifie
l'équation différentielle:
![\[y'(t)+\dfrac12y(t)=10\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009/4.png)
La température est exprimée en degrés Celsius ( C)
et le temps
C)
et le temps 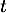 en heures.
en heures.
D'après Bac S, Antilles-Guyane, 23 juin 2009
Cacher la correction
La température est exprimée en degrés Celsius (
- Déterminer
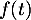 pour
pour  , sachant que pour
, sachant que pour  ,
la température de l'objet est 220
,
la température de l'objet est 220  C.
C.
- Pour la suite, on prendra comme fonction
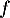 ,
la fonction suivante définie sur
,
la fonction suivante définie sur  par
par
![\[f(t)=200e^{-\frac{t}2}+20\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009/13.png)
On note sa courbe représentative.
sa courbe représentative.
- Étudier les variations de la fonction
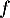 sur
sur 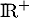 .
.
- Étudier la limite de la fonction
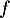 en
en 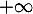 .
La courbe
.
La courbe 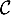 admet-elle une asymptote en
admet-elle une asymptote en 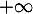 ?
?
- Représenter graphiquement
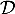 .
.
- Étudier les variations de la fonction
- Déterminer le moment où la température de l'objet est 50
 C.
C.
Donner une valeur approchée de ce moment en heures et minutes.
Correction exercice 2
D'après Bac S, Antilles-Guyane, 23 juin 2009
- Les solutions de l'équation différentielle:
sont
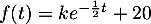 , pour tout réel
, pour tout réel 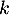 .
.
On sait de plus que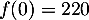 ,
soit
,
soit 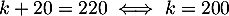 .
.
Ainsi, la température de l'objet est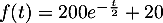 .
.
-
- Comme
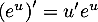 ,
on a
,
on a
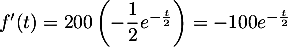 .
Comme
.
Comme 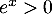 pour tout réel
pour tout réel 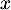 , on trouve donc
que
, on trouve donc
que 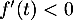 et donc que
et donc que 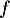 est strictement décroissante.
est strictement décroissante.
- On a
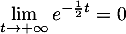 et
donc
et
donc 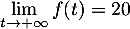 ,
et donc la droite d'équation
,
et donc la droite d'équation 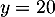 est asymptote
en
est asymptote
en 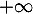 à
à 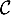 .
.
-
![\[\psset{xunit=1cm,yunit=.02cm,arrowsize=8pt}
\begin{pspicture}(-1,-20)(10,280)
\psline{->}(-.5,0)(8,0)
\psline{->}(0,-5)(0,280)
\psplot[linecolor=blue]{0}{8}{200 2.718 -.5 x mul exp mul 20 add}
\rput(1.3,150){\blue$\mathcal{C}$}
\psline(-.1,20)(8,20)
\rput(1.3,32){$\mathcal{D}$}
\rput[r](-.2,21){$20$}
\rput[r](-.2,220){$220$}
\multido{\i=1+1}{7}{\psline(\i,-5)(\i,5)\rput(\i,-15){\i}}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009_c/17.png)
- Comme
- Le moment
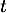 où la température de l'objet est 50
où la température de l'objet est 50  C
est
C
est
![\[\begin{array}{lcl}
&&f(t)=200e^{-\frac{t}2}+20=50\\[1em]
&\iff&
e^{-\frac{t}2}=\dfrac{30}{200}=\dfrac{3}{20}\\[1em]
&\iff&
-\dfrac{t}2=\ln\lp\dfrac3{20}\rp\\[1em]
&\iff&
t=-2\ln\lp\dfrac3{20}\rp\simeq3,8\enar\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009_c/20.png)
soit environ 3 heures et 48 minutes.
Cacher la correction
Exercice 3: Equation différentielle du 1er ordre - Convexité de la solution
On considère l'équation différentielle
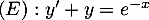 .
.
D'après Bac S, métropole, 22 juin 2010
On considère l'équation différentielle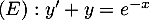 .
.
Cacher la correction
- Montrer que la fonction
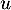 définie sur
définie sur 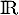 par
par
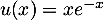 est une solution de l'équation différentielle
est une solution de l'équation différentielle 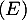 .
.
- On considère l'équation différentielle
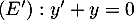 .
Résoudre l'équation différentielle
.
Résoudre l'équation différentielle 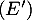 .
.
- En déduire toutes les solutions de l'équation différentielle
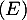 .
.
- Déterminer l'unique solution
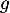 de l'équation différentielle
de l'équation différentielle 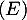 telle que
telle que 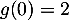 .
.
- Étudier la convexité de
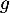 sur
sur 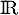 .
.
Correction exercice 3
D'après Bac S, métropole, 22 juin 2010
On considère l'équation différentielle
-
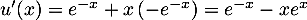 et donc
et donc
![\[u'(x)+u(x)=e^{-x}-xe^{x}+xe^{-x}=e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/3.png)
ce qui montre que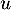 est bien solution de
est bien solution de 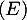 .
.
- Les solutions de
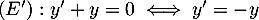 sont les fonctions définies par
sont les fonctions définies par
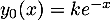 , pour tout réel
, pour tout réel 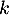 .
.
- Les solutions de l'équation différentielle
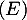 sont alors
sont alors
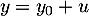 , soit, pour tout réel
, soit, pour tout réel 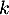 ,
,
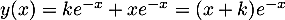 .
.
-
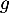 est une solution, donc
est une solution, donc 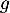 s'écrit sous la forme
s'écrit sous la forme
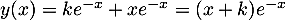 .
.
De plus,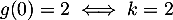 ,
d'où
,
d'où 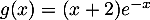 .
.
-
![\[g'(x)=-g(x)+e^{-x}=-(x+2)e^{-x}+e^{-x}=-(x+1)e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/18.png)
Pour calculer la dérivée seconde, on peut soit dériver à nouveau ce produit, soit utiliser l'équation différentielle. Comme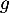 est solution de
est solution de 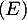 , on a
, on a
![\[g'(x)=-g(x)+e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/21.png)
et donc, en dérivant
![\[g''(x)=-g'(x)-e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/22.png)
soit,
![\[g''(x)=(x+1)e^{-x}-e^{-x}=xe^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/23.png)
Comme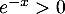 pour tout réel
pour tout réel 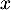 , on obtient donc
que pour
, on obtient donc
que pour 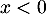 ,
, 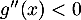 et donc
et donc 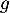 est concave,
et pour
est concave,
et pour 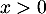 ,
, 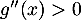 et donc
et donc 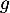 est convexe.
est convexe.
Enfin la courbe de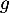 admet un unique point d'inflexion en
admet un unique point d'inflexion en 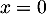 .
.
Cacher la correction
Exercice 4: Changement de variable dans une équation différentielle
Se ramener à une équation différentielle connue
On considère l'équation différentielle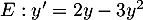 .
.
On cherche une solution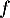 de cette équation telle que
de cette équation telle que 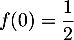 .
.
Cacher la correction
On considère l'équation différentielle
On cherche une solution
- Supposons que
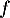 soit une solution de l'équation différentielle
soit une solution de l'équation différentielle 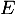 .
.
On pose alors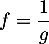 , en supposant que la fonction
, en supposant que la fonction 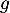 ne s'annule pas,
et on note
ne s'annule pas,
et on note 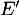 l'équation
l'équation 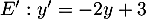 .
.
Montrer que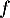 solution de
solution de 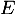 si et seulement si
si et seulement si 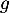 solution de
solution de 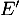 .
.
-
- Préciser la valeur de
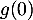 .
.
- Déterminer la solution
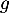 de l'équation
de l'équation 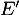 .
.
- En déduire la solution
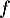 de
de 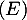 .
.
- Préciser la valeur de
Correction exercice 4
- Pour
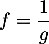 , on a
, on a 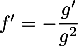 .
.
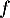 solution de
solution de 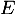 signifie que
signifie que 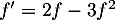 ,
,
soit donc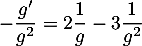 .
.
Comme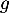 ne s'annule,
ne s'annule, 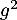 non plus, et on peut multiplier cette équation par
non plus, et on peut multiplier cette équation par 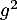 , pour obtenir l'équation
, pour obtenir l'équation
 qui montre que
qui montre que 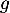 est solution de l'équation
est solution de l'équation 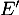 .
.
-
- On a
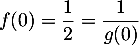 et donc
et donc 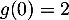 .
.
- L'équation
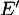 se résout simplement: c'est une équation différentielle linéaire à coefficients constants de solution
se résout simplement: c'est une équation différentielle linéaire à coefficients constants de solution
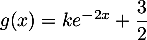 .
.
Comme on a vu que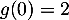 , on a alors
, on a alors 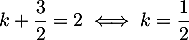 ,
d'où
,
d'où 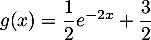 .
.
- On revient enfin à l'équation
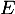 par la transformation
par la transformation
![\[\begin{array}{ll}f(x)&=\dfrac1{g(x)}\\
&=\dfrac1{\dfrac12e^{-2x}+\dfrac32}\\
&=\dfrac2{e^{-2x}+3}\enar\]](/Generateur-Devoirs/TS/ChapEqDiff/chgtvar_c/21.png)
qui est donc la solution recherchée de l'équation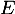 .
.
- On a
Cacher la correction
Quelques autres devoirs
sur les équations différentielles: désintégration de noyaux radioactifs - Température de refroidissement d'un objet (Bac S, Antilles-Guyane, 23 juin 2009) - Équaton différentielle avec changement de fonction (Bac S, métropole, 22 juin 2010) - Équaton différentielle non linéaire, avec un carré
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité - Probabilités & loi binomiale - Suite récurrente
sur la résolution d'&quations différentielles
Voir aussi: